あの「微積物理」を無料で学べます！！
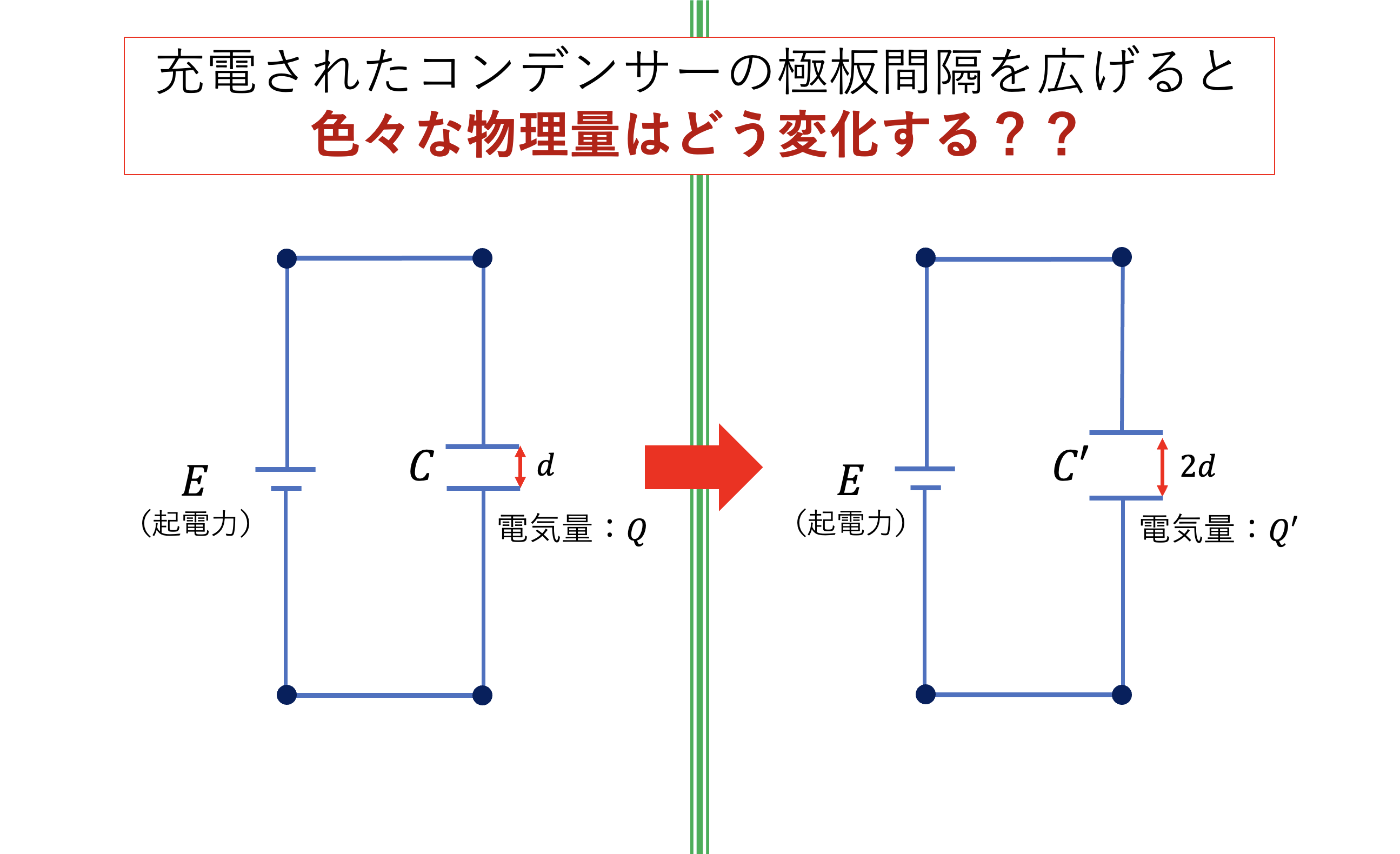
この記事ではコンデンサーについて、
その極板間の距離を広げる場合の
- 電位差の変化
- 電気量の変化
- 静電エネルギーの変化
について網羅的に解説していきます。
今回の内容を何も見ずに人に説明できるようになれば、
コンデンサーの極板を広げる場合の問題は
完璧と行っても過言ではないので
しっかりとマスターしてください！
ただし、長いので、
適宜必要な時に必要な箇所を見てみる、
という風にしてもらえればと思います。
また、今回の内容ではコンデンサーの基礎的な内容の説明はしません。
なので、その点に自信がない方は
以下の記事でまずコンデンサーの基礎知識を固めるようにしましょう。
Contents
コンデンサーを広げた場合の電位差の変化
それではまず、
コンデンサーを広げた場合の
電位差の変化
について解説していきます。
電池に接続されている時
まず考えるのは
このように、コンデンサーと電池が接続された状態で
コンデンサーの極板の感覚を広げる場合です。
電池と接続されている、ということは
電池と同じ電圧（電位差）が
極板間にも生じている
ということなので、話は簡単です。
電池の起電力を$E$、
コンデンサーの電圧を$V$と書くと、
極板の間隔を広げても、電位差は変わらず
$$\large V = E$$
となります。
電池に接続されていない時
では次に、
電池に接続されていない場合の
電位差の変化
を考えていきます。
電池に接続されてない、ということは、、？
先ほどは電池に接続されていたために
コンデンサーの電位差は電池の起電力に等しくなることを見ました。
ということは、先ほどとは違い今回のように
電池に接続されていない場合には、当然
電位差が極板を広げる前後で
変わってしまう
ということが予想できるわけですが、
この時、それよりも意識してほしいのが
電源と接続されていないため
極板を広げる前後で
コンデンサーの電荷は移動できない
ということです。
そして、今回はこれを利用して
電位差の変化を追うことにします。
物理では往々にして
ある操作の前後での
何らかの物理量の変化を考える
ということをします。
（今回の場合で言えば「極板を広げる前後での電位差の変化」）
このような場合、
操作の前後で「不変な量」に注目し、
それを利用して
考えたい物理量の変化を追う
というのが一般的に有効です。
「不変な量」としてよくあるのが
「力学的エネルギー」（力学的エネルギーの保存）であり、
今回の場合には不変な量として「電荷」を使います。
物理の量の変化を追いたい、という場合には
このことを思い出し、
「操作の前後で不変な量は何か？」
を考えるといいです。
電荷の量が不変であることを利用して電位差の変化を追う
では、実際に電位差の変化を追っていきましょう。
再度以下に示すようにスイッチ$S$を閉じて
起電力$E$の電池と接続し、充電したコンデンサーから
スイッチ$S$を開けた状態で
極板間を$d$から$2d$に広げる場合を考えます。
コンデンサーの電気容量$C$は
$$\large C = \frac{\epsilon_0S}{d}$$
$$\epsilon_0 : 誘電率,~S: 極板の面積,~ d : 極板間距離 $$
という式で書けることを思い出すと、
今、極板間の距離が
$$\large d→2d$$
と変化するので、電気容量自体は
$$\large C → \frac{1}{2}C$$
（最初のコンデンサーの電気容量を$C$とおいた）
というように、元の半分の大きさになります。
また、コンデンサーの関係式：
$$\large Q = CV$$
と、
電荷$Q$が極板を広げる前後で不変
であることに注意すると、
$$\large Q = C’V’= CV$$
（$C’$：操作後の電気容量
$V’$：操作後のコンデンサーの電圧）
（電荷$Q$は極板を広げる前と変わっていないことに注意）
を得ることができます。
このうち、2つ目の「＝」について
「$V’ = $」の形に変形すると、
$$\large V’ = \frac{C}{C’}V$$
を得ます。
そして、先ほど述べたように、電気容量の変化は
$$\large C → \frac{1}{2}C = C’$$
と書けるので、これを$C’$に代入することにより、
$$\large V’ = \frac{2Q}{C} = 2V$$
（最後の等式では”極板を広げる前”のコンデンサーの関係式$Q = CV$を使用）
という結果が最終的に得られます。
つまり、
広げる前の電位差$V$の2倍になる
という結果を得ることができます。
この結果が得られたのは
あくまで、
極板間距離を2倍にする時
という特定の場合であることを忘れないようにしましょう。
コンデンサーを広げる場合の電気量の変化
次に、
コンデンサーを広げる場合の
電気量の変化
を考えていきましょう。
状況として、充電されたコンデンサーの極板間の距離を
$d$から$2d$へ広げることを考えます。
電池に接続されていない時
電池に接続されていない場合は簡単です。
状況としては、次の図のように
コンデンサーを充電した後スイッチを開きます。
そして、この状態でコンデンサーの極板の距離を広げることを考えます。
コンデンサーに充電される電荷というのは
電池から供給される電荷です。
従って、
電荷を供給してくれる
電池と繋がっていない
ということは
コンデンサーの電荷は
操作の前後で変化しない
と言い換えることができます。
そのため、広げる前の電荷を$Q$
広げた後の$Q’$と書くと、
$$\large Q = Q’$$
を得ることができます。
簡単ですね。
電池に接続されている時
次は、
電池に接続されたまま、
コンデンサーを広げた場合の
電荷の変化
を考えます。
今回は、先ほどの電池に接続されている場合と違って
電荷の量は、コンデンサーを広げる前後で変化します。
この変化を考える際に注目してほしいのが
コンデンサーの電位差$V$は
広げる前後で変化しない
ということです。
すでに述べましたが大事なので、
もう一度言及しておきます。
物理では、往々にして
ある操作の前後での
何らかの物理量の変化を考える
ということをします。
（今回の場合で言えば「極板を広げる前後での電荷の変化」）
このような場合、
操作の前後で「不変な量」に注目し、
それを利用して
考えたい物理量の変化を追う
というのが一般的に有効です。
「不変な量」としてよくあるのが
「力学的エネルギー」（力学的エネルギーの保存）であり、
今回の場合には不変な量として「電位差$V$」を使います。
物理の量の変化を追いたい、という場合には
このことを思い出し、
「操作の前後で不変な量は何か？」
を考えるといいです。
コンデンサーの電位差が不変であるということは、
広げた後の物理量に「’」をつけると
コンデンサーの関係式から
$$\large V = \frac{Q}{C} = \frac{Q’}{C’}$$
が成り立つことを意味します。
そして、この等式を変化後の電荷を求めるために
2つ目の等号について「$Q’ = $」という形に変形すると、
$$\large Q’ = \frac{Q}{C}C’$$
という表式を得ることができます。
ここで、広げた後のコンデンサーの電気容量$C’$は
電気容量の表式
$$\large C = \frac{\epsilon_0S}{d}$$
において、$d→2d$とすればよく、
それはつまり、
$$\large C →C’=\frac{1}{2}C$$
と電気容量が変化することを意味します。
これを先ほどの広げた後の電荷$Q’$の表式に代入して
\begin{align}
\large Q’ &\large= \frac{Q}{C}\cdot \frac{1}{2}C\\
\\
&\large =\frac{1}{2}Q
\end{align}
という結果を得ることができます。
つまり、コンデンサーの電荷は
極板の間隔を2倍に広げると、
元の半分に減少するわけです。
この結果が得られたのは
あくまで、
極板間距離を2倍にする時
という特定の場合であることを忘れないようにしましょう。
極板間距離を$x$倍にする時にに
これまでと同様の議論をすれば問題ありません。
コンデンサーを広げる場合の静電エネルギーの変化
次に、
コンデンサーを広げると
コンデンサーの静電エネルギーが
どのように変化するか
をみていきましょう。
状況としては、これまでのように
コンデンサーの極板の間隔を$d$から
$2d$に広げることを考えます。
大事なので、再々度言及しておきます。
物理では、往々にして
ある操作の前後での
何らかの物理量の変化を考える
ということをします。
（今回の場合で言えば「極板を広げる前後でのエネルギーの変化」）
このような場合、
操作の前後で「不変な量」に注目し、
それを利用して
考えたい物理量の変化を追う
というのが一般的に有効です。
「不変な量」としてよくあるのが「力学的エネルギー」（力学的エネルギーの保存）です。
物理量の変化を追いたい、
という場合にはこのことを思い出し、
「操作の前後で不変な量は何か？」
に着目するといいです。
以下もこの考え方を使っていきます。
電池に接続されている時
まず以下のように、回路にスイッチを追加し、
スイッチを閉じたまま
極板を広げていく
ことを考えます。
この操作の前後で不変な量はなんでしょうか？
今回の場合であれば「電池に接続されているので」
不変な量はコンデンサーの電位差$V$ですね
そこでコンデンサーの電位差$V$を、
コンデンサーのエネルギー$U$を使って表してみましょう。
コンデンサーのエネルギーの式は
$$\large U = \frac{1}{2}CV^2$$
と書くことができるので、
$V = $の形に変形して、
$$\large V = \sqrt{\frac{2U}{C}}$$
と書けます。
広げた後の物理量に「’」をつけて表すことにすると、
操作の前後で電位差は不変であることに気をつけて
$$\large V = \sqrt{\frac{2U}{C}} = \sqrt{\frac{2U’}{C’}} $$
今知りたいのは、操作後のエネルギー$U’$なので、
2つ目の等号について、$U’$について解くことにより、
$$\large U‘ =\frac{C’}{C}U $$
を得ることができます。
広げた後のコンデンサーの電気容量$C’$は
$$\large C = \frac{\epsilon_0S}{d}$$
という電気容量の式から、
今は極板間の距離を2倍にしているため、
$$\large C’ = \frac{1}{2}C$$
と書けます。
これを先ほどの$U’$の式に代入して
$$\large U’ = \frac{1}{2}U$$
という結果を得ることができます。
つまり、
エネルギーは元の半分になるわけです。
電池につながれている場合
極板間の距離を2倍にすると
コンデンサーのエネルギーは1/2倍になる
ということがわかります。
先ほどは
$$\large U = \frac{1}{2}CV^2$$
という表式を使いましたが、
この式ではなく、
$$\large U = \frac{1}{2}QV$$
というコンデンサーのエネルギーの表式を用いても構いません。
その場合、先ほどと同様に
「極板を広げた後の物理量」に
「’」をつけて表すことにすると、
電圧が操作の前後で不変であることから、
$$\large V = \sqrt{\frac{2U}{Q}} = \sqrt{\frac{2U’}{Q’}} $$
となり、これを$U’$について解けばいいことになります。
この際、操作後の電荷については、
上でやったように、
$$\large Q’ = \frac{1}{2}Q$$
（電池に接続されたまま、極板を広げた場合の電荷の変化）
とわかっているので、これを用いて
$$\large U’ = \frac{1}{2}U$$
という同様の結果を得ることができます。
電池に接続されていない時
では次に
電池に接続されてない状態で
極板を広げた場合の
エネルギーの変化
を考えていきます。
この場合、操作の前後で不変な量はなんでしょうか？
それは
コンデンサーの電荷$Q$
です。
ということで、コンデンサーの電荷$Q$を
コンデンサーのエネルギー$U$で使った表してみましょう。
まず、コンデンサーのエネルギー$U$は
電荷$Q$を用いて
$$\large U = \frac{Q^2}{2C}$$
と書けます。
これを「$Q = $」の形に変形して、
$$\large Q = \sqrt{2CU}$$
を得ることができます。
この表式と、電荷が操作の前後で不変であることから、
広げた後の物理量に「’」をつけて表すことにすると
$$\large Q = \sqrt{2CU}= \sqrt{2C’U’}$$
を得ることができます。
今求めたいのは、
操作後のコンデンサーのエネルギー$U$なので、
2つ目の等号について「U’=」の形に整理することにより、
$$\large U’ = \frac{C}{C’}U$$
を得ることができます。
また、今極板間の距離を$d→2d$
という風に2倍にしているので、
コンデンサーの電気容量の式：
$$\large C = \frac{\epsilon_0 S}{d}$$
（$\epsilon_0$：真空の誘電率, $S$：極板の面積, $d$：極板間の距離）
より、
$$\large C’ = \frac{1}{2}C$$
を得ることができます。
これを先ほどの$U’$の式に代入することにより、最終的に、
$$\large U’ = 2U$$
という結果を得ることができ、このことから
電池につながれてない場合、
極板間の距離を2倍にすると
コンデンサーのエネルギーは2倍になる
ということがわかります。
コンデンサーを広げた場合の電流の変化
それでは最後に、
コンデンサーの極板を広げた場合の変化について
より詳しくなるために、
コンデンサーを広げる場合の
電流の変化
について考えていきます。
基本的にコンデンサーの極板間隔を広げている最中の
電流の定量的な変化は高校物理では扱いません。
なので、以後は定性的な話がメインになります。
電池に接続されない場合には電流は流れない（当然）
まず、電池に接続されていない場合についてです。
電流というのは無条件にいつでも流れるわけではありません。
当たり前のことではありますが、
ちゃんと
電荷が移動できる
場所があって初めて
電流は流れることができます。
電池に接続されていない場合には、
電荷が移動できる先がない、
ということなので、電流は流れません。
加えて、電流が流れない、ということは
コンデンサーに
溜まった電荷は変化しない
ということを忘れないようにしてください。
（この事実を「コンデンサーの電荷を不変量とする場合」に使いました）
コンデンサーを広げた場合の電流の向きの決め方
では、次に電池と接続されている場合について考えていきます。
この場合、電荷が移動できる先があるので
極板の間隔を広げると当然電流が流れます。
電荷を含めて図示すると次のようになります。
既に上の方で考えたように、
この場合のコンデンサーの電荷は
$$\large Q→Q’ = \frac{1}{2}Q$$
のように、最初の電荷の半分に減少します。
つまり、これだけの変化を引き起こす電荷が
コンデンサー側から
電池に向かって移動した
（電流が流れた）
ことになります。
電流の担い手は
マイナスの電荷をもった電子
であることに気をつけると、
コンデンサーの極板のうち
マイナスに帯電している側から
負電荷が流出し、
プラスに帯電している側へ
負電荷が流入する
ことになるので
図示すると、次の図のようになります。
この時、移動した電荷の総量について、
コンデンサーから減った電荷の分だけ移動することに注意してください。
つまり、コンデンサーの電荷の変化分が電流として流れることになります。
極板を変化させる問題と対峙する時は、色んな視点で眺めることができるように
ここまでコンデンサーの極板間隔を広げる場合について
色々な物理量に注目して考えてきした。
実際に問題に取り組む際には、ここでの議論を参考に
- 電荷の量はどうなっているか
- 電位差の変化はどうなっているか
- コンデンサーのエネルギーはどうなっているか
- 電流はどういう向きに流れているのか
と、色々な視点で考えることを訓練してください。
絶対に
1つの側面からしか考えない
といったことがないようにしましょう。
色々な物理量の視点の切り替えが
スムーズにできるようになれば
状況が複雑になった応用問題にも対応できるようになります。
極板間の間隔を変える際に一貫して有用な指針
また、極板間の間隔を変える際に
一貫して有用な指針は
操作の前後で「不変な量」に着目し
それを利用して
求めたい物理量の変化を調べる
というものでした。
これは、今回の場合のみならず
極板を狭くする場合、また
必ずしも2倍に広げるわけではない場合、
さらには、より一般に
ある操作の前後で物理量の変化を考える場合に有効なので
覚えておくといいでしょう。
まとめ
それでは今回のまとめです。
- コンデンサーの極板間隔を変化させるような場合には
「操作の前後で不変な物理量」に着目して、それを利用し、
求めたい物理量の変化を調べる、が基本方針！ - この方針は「ある操作の前後での物理量の変化を考える」場合に
一般的に有効なので覚えておくと良い！ - 丁寧に説明してきましたが、瞬時にこれらを頭の中から取り出せるように！
あの「微積物理」を無料で学べます！！
皆さんの「ここを教えてほしい」を募集しています！
高校物理に関して
「こんなことを教えて欲しい」
「この問題をわかりやすく解説して欲しい！」
「勉強のコツを知りたい！」
などなど、質問を募集しています！
気軽に質問してください！無料です！
質問内容に関しては記事として回答させていただきます！
⚠️質問の回答は先着順で回答していくため、質問から回答までの期間が長くなることがあります。あらかじめご了承ください。
コメントを残す