同じ質量の弾性衝突ではなぜ「速度の入れ替わり」が起こる？質量が違う場合の弾性衝突は？

今回は、完全弾性衝突において

質量の異なる物体の衝突
における速度の変化

について解説し、さらに

２物体の速度の入れ替わりが
なぜおこるのか

また、

どんな時に起こるのか

について解説していきます！

「（完全）弾性衝突」とは？

では、まず言葉の定義から解説していきます。

完全弾性衝突

もしくは

弾性衝突

というのは、

このように、

「衝突後の速度の差」と
「衝突前の速度の差」が
同じになる衝突

のことを言います。

これはあくまで速度の「大きさ」についての話であって、

衝突の前後での速度の「向き」の変化は
別で考える必要がある

という点に注意してください。

そして、この（完全）弾性衝突というのは
反発係数$e$を用いて説明すると、

$$-\frac{衝突後の速度差}{衝突前の速度差} = e = 1$$

$$(0 \leqq e \leqq 1)$$

（$e=1$の時、（完全）弾性衝突、$e=0$の時、完全非弾性衝突（合体））

とこのように、反発係数が$1$になる衝突のことを指します。

質量の異なる2物体の（完全）弾性衝突

それでは、質量の異なる2物体の弾性衝突について
例題を通して考えていきます。

例題

考え方の基本的な方針

衝突の前後で物体の運動を考える場合には

の３ステップを踏むことが基本になります。

以上の内容が基本方針になります。

解説

では、実際に式を作っていきましょう。

①反発係数$e$を用いた関係式

今、（完全）弾性衝突を考えており、
反発係数が

$$\Large e = 1$$

だとわかっているので、この反発係数を用いた速度の関係式を作ります。

反発係数の定義式：

$$\large -\frac{(衝突後の速度差)}{(衝突前の速度差)} = e $$

に、

$$\large (衝突前の速度差) = v_2 – v_1$$

$$\large (衝突後の速度差) = v_2’ – v_1’$$

$$\large e = 1$$

を代入して、

\begin{align}
-\frac{v_2′-v_1′}{v_2-v_1}& = 1\\
-(v’_2-v’_1)&=v_2-v_1\tag{1}
\end{align}

という式を得ることができます。

②運動量保存則の関係式

次に運動量保存則から、

\begin{align}
mv_1’+Mv’_2 &= mv_1 +Mv_2 \tag{2}\\
（衝突後の運動量）&= （衝突前の運動量）
\end{align}

という式を得ることができます。

③2つの式を連立する

改めて、得られた2つの式を並ます。

\begin{align}
-(v’_2 – v’_1)&= v_2 – v_1\tag{1}\\
\\
mv’_1 + Mv’_2 &= mv_1 + Mv_2\tag{2}\\
\end{align}

念の為述べておきますが、今
$v_1, v_2$が「既にわかっている量」であり、
$v_1’, v_2’$が「これから求めたい量」です。

やや面倒ですが、これらを連立していきます。

まず、$v’_2$から求めていきましょう。

(1)式より、

$$\large v’_1 = v’_2 + v_2 – v_1$$

と書くことができるので、
これを(2)式に代入し、変形していきます。

こうすることで、$v’_2$のみを含み、
$v’_1$を含まない式を得ることができるはずです。

\begin{align}
m(v’_2 + v_2- v_1) + Mv’_2 & = mv_1 + Mv_2\\
\\
(M+m)v’_2 &= -m(v_2 – v_1) + mv_1 + Mv_2\\
\\
(M+m)v’_2 &= 2mv_1+(M-m)v_2\\
\\
v’_2 &= \frac{2m}{M+m}v_1 + \frac{M-m}{M+m}v_2
\end{align}

と$v’_2$を求めることができます。

さらに、この$v_2’$の式を(1)式に代入することにより、

\begin{align}
-\Big(\frac{2m}{M+m}v_1 &+ \frac{M-m}{M+m}v_2-v’_1\Big) = v_2 – v_1\\
\\
v’_1 &= \Big(\frac{2m}{M+m}-1\Big)v_1 + \Big(\frac{M-m}{M+m}+1\Big)v_2\\
\\
v’_1&=-\frac{M-m}{M+m}v_1 + \frac{2M}{M+m}v_2\\
\end{align}

と$v’_1$を求めることができます。

以上で、問題を解くことができました。

エネルギーの変化を見てみる

例題を解くことができたわけですが、
念の為、エネルギー保存則がちゃんと成り立っているかを確認してみましょう。

もし、エネルギー保存則がちゃんと成り立っているのなら、

\begin{align}
\frac{1}{2}mv^2_1+\frac{1}{2}Mv^2_2 = \frac{1}{2}mv’^2_1+\frac{1}{2}Mv’^2_2 \tag{3}
\end{align}

という式がなりたつはずです。

式変形が面倒ですが、例題によって得られた解を用いて
(3)式が成り立つかを確認していきます。

例題で得られた$v_1$と$v_2$を再度並べます。

$$v’_1 = -\frac{M-m}{M+m}v_1 + \frac{2M}{M+m}v_2 $$

$$\large v’_2 = \large\frac{2m}{M+m}v_1 + \frac{M-m}{M+m}v_2$$

これらの結果をエネルギーの式に代入していきます。
まず$mv’^2_2$について、
$v’_2$の表式を代入し、$v_1, v_2$のみの式にしましょう。

\begin{align}
mv’^2_1 &= \frac{m(M-m)^2}{(M+m)^2}v_1^2 – \frac{2mM(M-m)}{(M+m)^2}v_1v_2 + \frac{4mM^2}{(M+m)^2}v_2^2\\
\\
&=  \frac{1}{(M+m)^2}\Big(m(M-m)^2 v_1^2 – 2mM(M-m)v_1v_2 + 4mM^2 v_2^2\Big)
\end{align}

（式変形が大変かもしれませんが、頑張ってください）

今度は$Mv’^2_2$について$v’_2$の表式を代入して、
$v_1, v_2$のみの式にします。

\begin{align}
Mv’^2_2 &= \frac{4m^2M}{(M+m)^2} + \frac{2mM(M-m)}{(M+m)^2}v_1v_2 + \frac{M(M-m)^2}{(M+m)^2}v^2_2\\
\\
& = \frac{1}{(M+m)^2}\Big(4m^2Mv_1^2 + 2mM(M-m)v_1v_2 + M(M-m)^2v_2^2\Big)
\end{align}

とかけるので、これを(3)式の右辺に代入していきます。

すると、

\begin{align}
\frac{1}{2}mv’^2_1 + \frac{1}{2}Mv’^2_2 &= \frac{1}{2(M+m)^2}\Big((m(M-m)^2+4m^2M)v_1^2 + (4mM^2 + M(M-m)^2)v_2^2\Big)\\
\\
& = \frac{1}{2(M+m)^2}\Big((m(M-m)^2+4m^2M)v_1^2+ (4mM^2 +M(M-m)^2)v_2^2\Big)\\
\\
& =  \frac{1}{2(M+m)^2}(M+m)^2(mv_1^2+Mv_2^2)\\
\\
& = \frac{1}{2}mv_1^2 + \frac{1}{2}Mv_2^2\\
\end{align}

とこのように、エネルギー保存則がちゃんと成り立っていることが確認できました。

今回は（完全）弾性衝突を考えていたので
このエネルギー保存則が成り立っていますが、

弾性衝突以外の場合（$e\neq 1$）
はエネルギー保存則は成り立たない

ということに注意して下さい。

質量が同じ2物体の（完全）弾性衝突：速度の入れ替わり

では、先ほどはちょっと状況を変えて、
質量が同じ物体の衝突では速度はどうなるでしょうか。

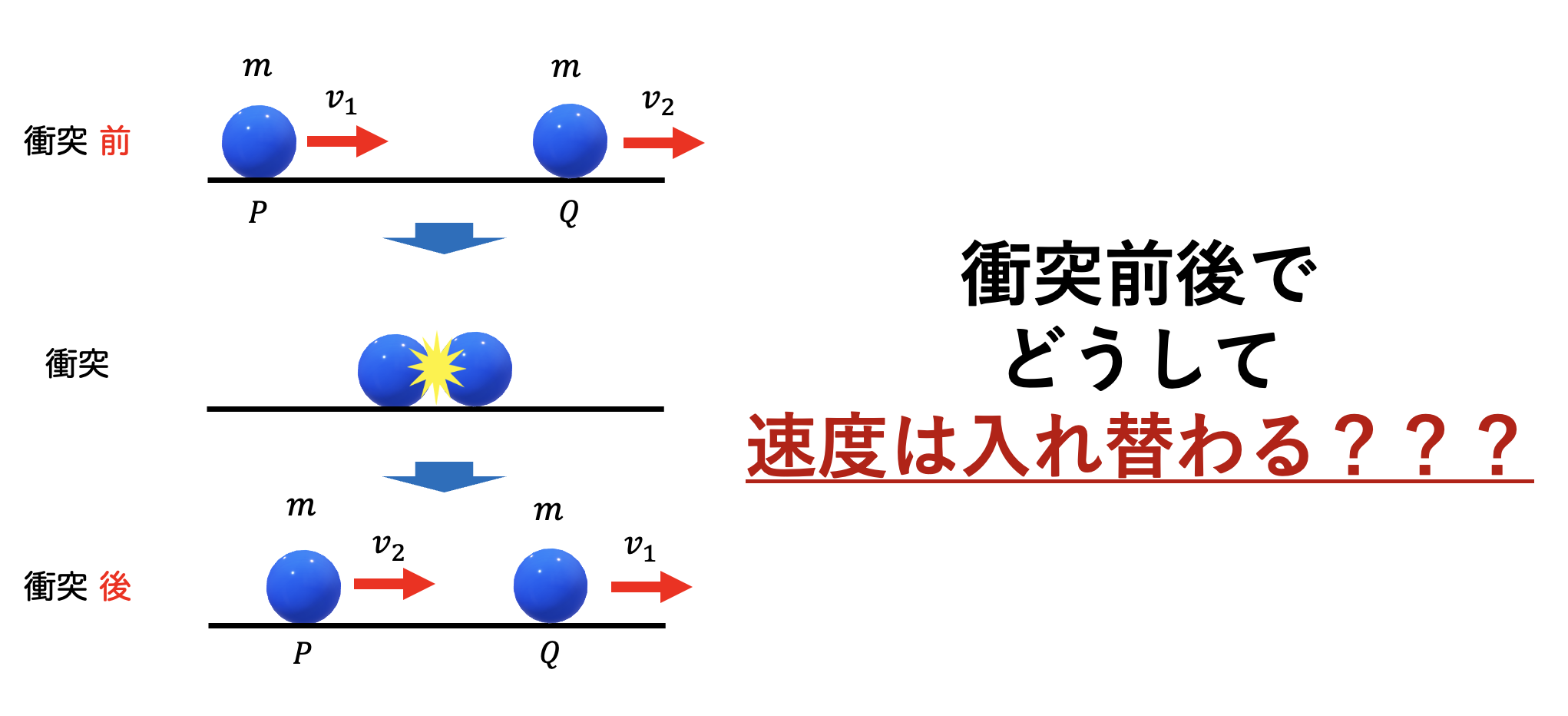
例題

問題

図のように、速度$v_1$で動く質量$m$の$P$が速度$v_2$で動く質量$m$の$Q$に（完全）弾性衝突した。

衝突後の速度$v’_1$、$v’_2$を求めよ。

解説

方針は質量が異なる場合と同じです。

今回は、反発係数の関係式から

\begin{align}
\large -(v’_2 – v’_1) &= \large v_2 – v_1\tag{4}\\
\end{align}

また、運動量保存則から

\begin{align}
\large mv’_1 + mv’_2 &= \large mv_1 + mv_2\\
\\
両辺を質量&mで割って\\
\\
\large v’_1 + v’_2 &= \large v_1 + v_2 \tag{5}\\
\end{align}

を得ることができます。

この(4)(5)式の2つを連立すると、

(4)式+(5)式より、

$$v’_1 = v_2$$

また、(4)式-(5)式より、

$$v’_2 = v_1$$

を得ることができます。

この結果は、質量が異なる場合の
$v’_1$と$v’_2$の式において
$M→m$と置き換える（質量を同じにする）ことでも得られます。

速度が入れ替わる条件・理由

上でやった簡単な計算結果から、
衝突する物体の質量が同じ場合には

衝突の前後で
速度が入れ替えが起こる

ことがわかります。

よく、質量が同じ物体の衝突を考える際に

なぜ、速度が入れ替わるの？？

という疑問を抱く人がいますが、
これまでの結果を見れもらえばわかるように、
速度の交換が起こる理由は

衝突する2つの物体の
質量が等しいから

としか言いようがありません。

一般の衝突の場合では速度の交換は起こりませんが、
そこで、質量を同じにする（$M→m$と変えることに対応）
と”結果的に”速度が交換されるという現象が導かれた、

という流れを意識するようにしてください。

まとめ

それでは今回のまとめです。