求む！今のうちにライバルと差をつけたい新受験生！
今回は、コンデンサーについてより理解を深められるように
コンデンサーの公式
また
電気容量の公式
について深掘りしていきます！
Contents
コンデンサーにおける公式（とその単位）
まず、今回星下げていく公式をとりあえず列挙していきます。
これらの公式を「導出」するのはやや難易度が高いです。
そのため「導出」に充てたこの記事の後半部分は
“余裕のあるの場合に”読むことをおすすめします。
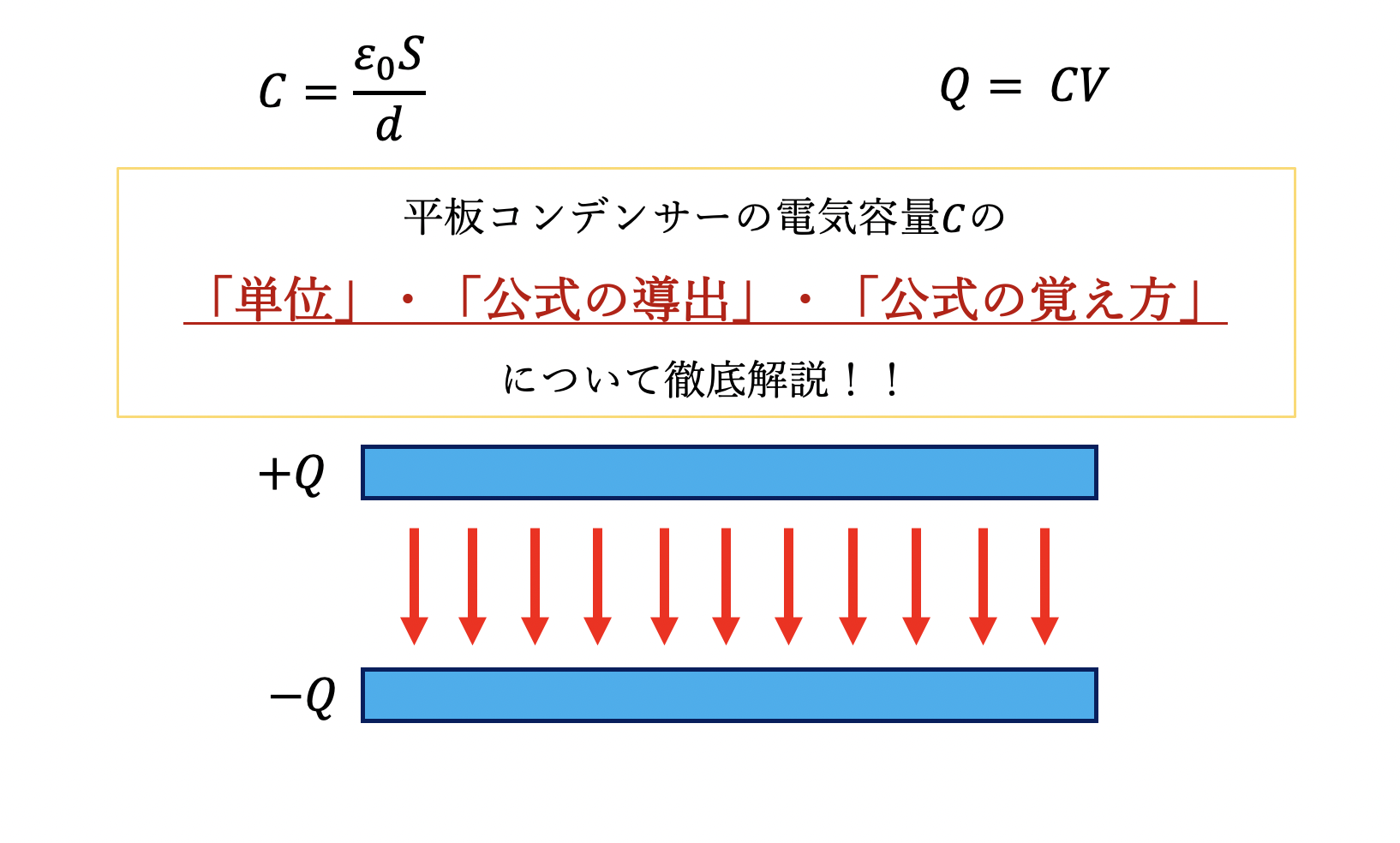
コンデンサーの関係式
コンデンサーの関係式というのは、
$$\large Q = CV$$
とこのように書くことができました。
この式は、コンデンサーが上図のような状況において
コンデンサーがどれぐらい
電荷$Q$を蓄えることができるか
を考える場合や、
もしくは変形することで、
ある量の電荷が溜まっている時の
極板間の電位差$V$
を求める際に使えます。
電気容量の式
そして、このコンデンサーというのは
電気容量$C$という量によって特徴づけられます。
「電気容量」について、
このようなコンデンサーに対して
電気容量$C$は
$$\large C = \epsilon_0 \frac{S}{d}$$
このように書かれます。
この式を使えば、
上図の電気容量$C$というのは
元の状態から
極板の面積を
より大きく（小さく）した場合には
より大きく（小さく）なる
さらに、
極板間の距離を
より大きく（小さく）した場合には
より小さく（大きく）なる
ということがわかり、
コンデンサーの状況が変化する場合に
その電気容量が
どう変化するか
を考える時に使えます。
コンデンサーの公式の覚え方
ここでは、先に挙げた公式を
頭に入りやすくなる覚え方について解説します。
コンデンサーの関係式の主人公は『電荷』
では、まずコンデンサーの関係式：
$$\Large Q = CV$$
からです。
この式自体は登場する文字もすくなく、
難しくはないですが、
電気容量$C$を$Q$にくっつけるのか
$V$にくっつけるのか、で迷わないように
気を付ける必要があります。
その混乱を防ぐために
コンデンサーの関係式というのは
電荷$Q$を
求めるための関係式である
ということを合わせて頭に入れるようにしてください。
そもそもこの電気容量$C$が
導入された経緯ですが、それは
ある電圧$V$をコンデンサーに加えたに
どれぐらいの電荷が貯まるんだろうか？
という謎を考える際に、
という感じです。
この流れを合わせてインプットしておき、
コンデンサーの関係式は
元々電荷$Q$を求めることが
モチベーションだ
ということを意識すれば、間違いなく
「$Q=$」という形の式に書きたくなると思うので
コンデンサーの関係式の
主人公は電荷Q
ということも合わせて頭に入れるようにしましょう。
電気容量の式
電気容量の式：
$$\Large C = \frac{\epsilon_0 S}{d}$$
というのは、何が分母に来て、
何が分子に来るのかなかなかに
混乱しやすいのではないかと思います。
おすすめの覚え方としては
downの「$d$」が下に、
イエス（イプシロン$\epsilon$とエス$S$）
が上にくる
というものです。
極板間の距離を表す
（downの）$d$だけが下に、
他は全部上に入ります。
このように覚えておけば
公式がどのように書けたかで間違いづらくなると思うので、有効活用してください。
コンデンサーの単位について整理
コンデンサー関連の公式を導出していく前に、
その単位についても少し話しておきます。
単位についてわかっておくと、
解答があっているかの確認の際に使えるので、
余裕があればで問題ないですが、頭に入れておくといいです。
コンデンサー$C$は
$$\Large F：ファラド$$
という単位で表されます。
これ自体は「覚えてください」という他ないですが、
コンデンサーの関係式
$$\large Q = CV$$
からわかるように、この「ファラド」という単位と
電荷、電圧の単位との関係は
\begin{align}
\large 1[C] &\large =1[F\cdot V]
\\
\\
\large 1\Big[\frac{C}{V}\Big] &\large =1[F]
\\
\end{align}
このようになります。
また、電気容量$C$が
$$\Large C = \frac{\epsilon_0 S}{ d}$$
でかけたので、この式において
それぞれの量の単位に注目し、
誘電率$\epsilon$の単位を$[\epsilon]$のように書くと、
\begin{align}
\\
\large [\epsilon_0] &\large = [C]\cdot \frac{[d]}{[S]}\\
\\
& \large = F \cdot \frac{m}{m^2}\\
\\
& \large =\frac{F}{m}
\end{align}
となり、誘電率の単位が[F/m]（ファラド毎メートル）だとわかります。
誘電率の単位を気にすることは少ないかもしれませんが、
聞かれたら導ける、ぐらいにはしておくといいです。
コンデンサーの公式の導出の仕方
それでは、いよいよコンデンサーに関する公式の導出を見ていきます。
初めにも言いましたが、この導出はやや難易度が高いので
余裕があれば読んでみる、ぐらいにしてください。
以降の内容がわからなくても心配いりません。
ただ、これらをわかっていて損もないので
よりコンデンサーの周りの知識を
緻密にしたい場合には、一通り流れを理解しておくことをお勧めします。
また、これ以降ではこちらの記事の内容がわかっていることが前提になっています。
（無限に広い）平面が作る電場
コンデンサーに関する公式を
導くためのスタート地点として、まず
（無限に広い）
平面が作る電場
を考えていきます。
というのもこの平面が作る電場というのが
コンデンサーの
片方の極板が作る電場
に対応するからです。
次の図のように、電荷が平面上に
無限に広く並んでいる状況を想像して下さい。
この平面に並んでいる電荷のうち、
1つの電荷に注目し、その1つの電荷が作る電場、
さらに、その周りの電荷が作る電場を書くと
次図のようになります。
このように全ての電荷は同じ電場を各々作ります。
その結果、電場というものは
矢印（ベクトル）として足し合わせることができるので、
（これを 「重ね合わせの原理」と言います）
矢印の横向きの成分は打ち消し合い、
最終的にに、
上向きと下向きの
電場しか残らない
という状態になります。
そして、これが
平面状に並べられた
電荷全てで起こる
ので、平面全体が作る電場というのは
上図のように、平面に対して垂直になります。
また、最初に言ったように
平面状に並んだ電荷というのは
コンデンサーの
片方の極板が作る電場
に対応するわけので、
とこのようになります。
ガウスの法則を使って平面が作る電場を求める
以上のように、平面が作る電場というのは
平面に対して垂直になる、ということがわかったので、
電場の表式を求めるために
ガウスの法則
を使います。
ガウスの法則については別の記事で
解説しているのでこちらを参照して下さい。
このガウスの法則にしたがって、
電場が垂直に貫く閉曲面を考えます。
今の場合、平面が作る電場が垂直に貫く閉曲面というのは
（電場が上か下にしか出ていないことを考えればわかるように）
図のような「直方体」となります。
図のように、直方体の上面と下面の面積を$S$としましょう。
そして、この直方体によって囲まれる
平面上の全電荷を$Q$とおきます。
すると、ガウスの法則から
平面が作る電場について、
$$\large E = \frac{Q}{2\epsilon_0 S}$$
という表式を得ることができます。
平面が作る電場について、
その式を見て貰えばわかるように
平面からどれだけ離れていようと
電場の大きさは一定
（その面積には依存する）
です。
平面からの距離が離れても
電場は変わらないって
おかしくないか？
と思うかもしれません。
その指摘は正しいです。
普通はこんなことは起こりません。
しかし、今は
無限に広い平面
という「超理想的な状況」を考えています。
なので、
「平面からの距離が離れても
電場は変わらない」となっても問題ないので安心してください。
逆の電荷を持つ2枚の平面を並べてみる
このように、1枚の平面が作る電場がわかりました。
当初の目的はコンデンサーの式を
考えることだったので、通常のコンデンサーのように
逆の電荷を持つ
2枚の平面（極板）を並べる
ことを考えましょう。
平面が作る電場というのは
上で述べたように、平面に対して垂直です。
また、正の電荷は吸い込むような電場を、
負の電荷は吐き出すような電場を作るので、
2 つの平面が作る電場を図示すると、
このようになります。
図示された電場について、
コンデンサーの間ではなく、
上側と下側にも
電場が存在する
ということに注意してください。
これらの存在は極板間引力を
考える際に重要になります。
この図から極板間では
正に帯電した平面からの電場と
負に帯電した平面からの電場が
同じ向きに強め合うことわかります。
それぞれの平面が作る電場は
$$\large E= \frac{Q}{2\epsilon_0 S}$$
で書くことができたので、
「極板間の電場」というのは
これを2倍したものであり、
$$\large E_{極板間} = 2E = \frac{Q}{\epsilon_0 S}$$
とこのようにかけます。
これで、コンデンサーの極板間の電場
の式が求まったことになります。
2枚の極板間の電位差は？
今まで「平面」と呼んできたのを
これからは「極板」と言い直します。
このような極板間の電場がわかったので
次に、この極板における
負に帯電した極板と
正に帯電した極板の電位差
を考えます。
重要なので、再度述べますが、
極板が作る電場というのは
（無限に広いという
理想的な状況を考えているので）
極板からの距離に関わらず一定
であることに注意してください。
電位差$V$というのは、
極板間の距離を$d$とすると
$$\large V =E\times (距離) $$
で求めることができたので、
図のように極板間の距離を$d$とすると、
極板間の電場の表式：
$$\large E_{極板間} = \frac{Q}{\epsilon_0 S}$$
を電位差の式に代入することで
極板間の電位差$V$として
$$\large V = \frac{Q}{\epsilon_0 S}\cdot d$$
を得ることができます。
コンデンサーの関係式と電気容量の式
$$\large V = \frac{Q}{\epsilon_0 S}\cdot d$$
このような電位差の式が得られた訳ですが、
今、最終的に欲しいのは「Q=」という、
蓄積できる電荷の量を表す式なので、
この式を
電荷$Q$を求める式
に書き直します。
すると、
$$\large Q = \frac{\epsilon_0 S}{d}\cdot V$$
と変形できます。
この時の電圧の係数：
$$\large \frac{\epsilon_0 S}{d}$$
が、コンデンサーの電気容量そのものであり、
それをあらためて$C$と書くことにすると、
$$\large C = \frac{\epsilon_0 S}{d}$$
$$\large Q = CV$$
という、最初に示した、
コンデンサーの
電気容量の式
と
コンデンサーの関係式
を導くことができました。
以上がコンデンサー関する公式の導出になります。
長かったですが、上の流れを頭に入れておけば
コンデンサーの問題に取り組む際に
混乱を最大限なくすことができ、
また、応用問題に取り組む際にも
戸惑うことを減らせるので
上記のことはしっかり、
一連の流れとして
頭に入れるようにしておくといいです。
まとめ
それでは今回のまとめです。
- 電気容量の関係式：$Q = CV$は
電荷$Q$を求めるための式！ - 電気容量の公式：$C = \frac{\epsilon_0S}{d}$は
「downのdが下に、”イエス”（イプシロン＋エス）が上に来る」で覚える！ - 電気容量の単位は「ファラド」であり、電荷を電圧で割ったものと同じ単位になる！
- 余裕があれば平板コンデンサーの電気容量$C$の導出の一連の流れを頭に入れておくと便利！
求む！今のうちにライバルと差をつけたい新受験生！
皆さんの「ここを教えてほしい」を募集しています！
高校物理に関して「ここがわからない」「この問題の解説が理解できない」などなど、質問を募集しています！
気軽に質問してください！
質問内容に関しては記事として回答させていただきます！
⚠️質問の回答は先着順で回答していくため、質問から回答までの期間が長くなることがあります。あらかじめご了承ください。
とりあえず、高い電圧を加えたら
貯まる電荷も大きくなる（比例）関係がある：
$$\large Q \propto V$$
（左の量が右の量に比例することを意味）
ことわかったから、とりあえず
その比例係数を$C$って置いとくか：
$$\large Q = CV$$