求む！今のうちにライバルと差をつけたい新受験生！
今回は、高校生にもわかるように、
電場を理解する上で何かと役立ち、
電場への解像度を何倍も上げてくれる
ガウスの法則
を解説していきます。
Contents
「ガウスの法則」とは？
「ガウスの法則」（簡易版）というのは
電場に関する法則で、以下の法則のことです。
電場というのは電荷があれば、四方八方に向けて発生し、
その向きは、
負電荷ならば吸い込むように、
正電荷ならば湧き出すように
発生する。
電荷が作る電場が垂直に貫くような
「電荷を囲む閉曲面」を考える。
この時、「電場が貫く閉曲面の面積$S$」と「電場$E$」の積が
「閉曲面内部の電荷の総和$Q$」を定数$\epsilon_0$で割ったものに等しい。
以上がガウスの法則です。
これは「法則」であり（定理ではない）
経験的に得られたものであるので、
なぜこの法則が成り立つか？
という疑問はあまり持たないで、
あるがままにこの法則を受け入れてください。
上記の法則を読んだだけでは
という人が大半だと思います。
ですが、とりあえずこのガウスの法則は
（もう一度いいますが）
「あるがままに」受け入れましょう。
ガウスの法則を使って電場を求めてみる
これからこのガウス法則を具体的にイメージしてもらうために、
2つの具体例について電場を考えていきます。
具体例１：点電荷が作る電場
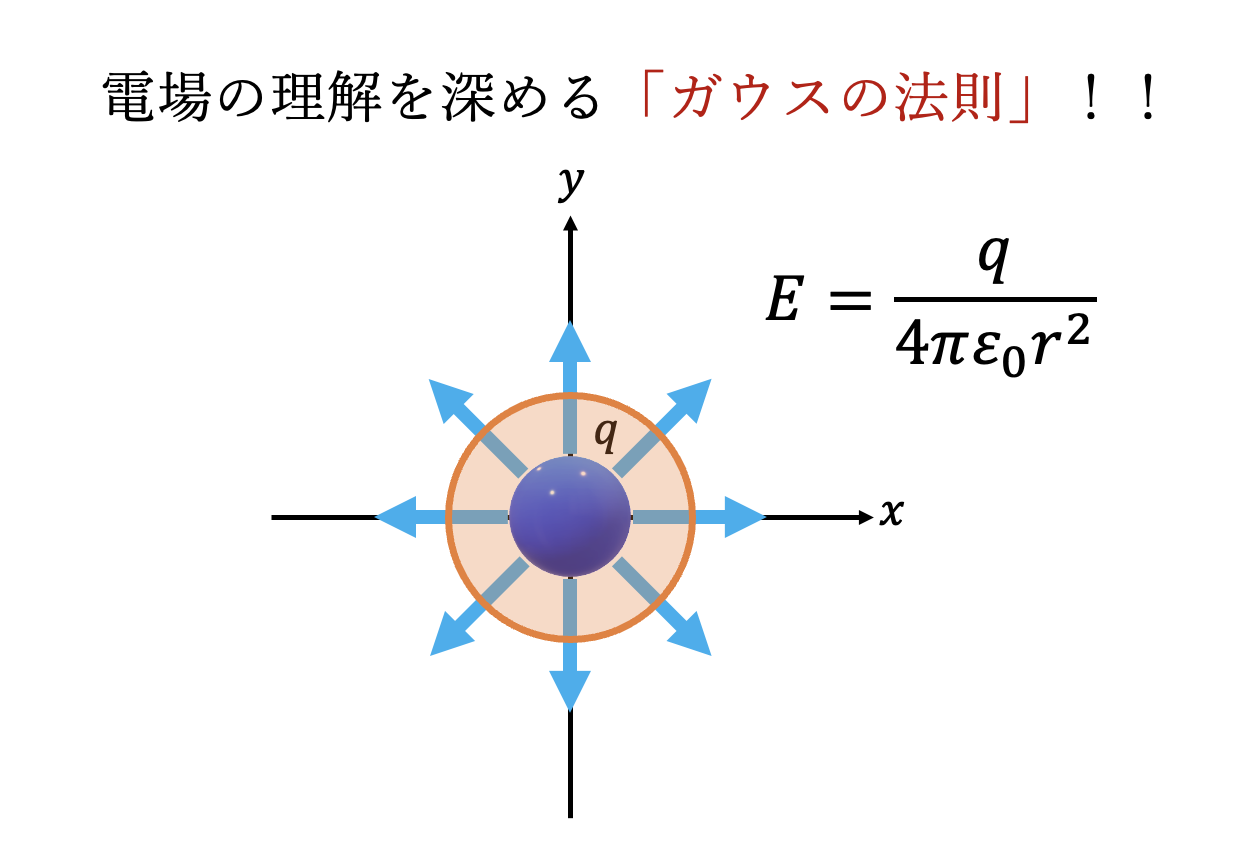
具体例1つ目は、次の図のような
1つの点電荷$q (> 0)$が作る電場
です。 
ステップ１：点電荷が作る電場の向きについて考える
ガウスの法則によれば、電場は電荷qから四方八方に発生し、
また、今考えている電荷は正電荷なので、
電場を書き込むと、次のようになります。
今は正電荷を考えていますが、
負電荷の作る電場を考える場合には、
電場の向きが反転することに気を付けると
このように書けます。
ステップ２：ガウスの法則を適用して電場を求める
再度、ガウスの法則を載せます。
電場というのは電荷があれば、
四方八方に向けて発生し、その向きは
負電荷ならば吸い込むように、
正電荷ならば湧き出すように
発生する。
電荷が作る電場が垂直に貫くような
「電荷を囲む閉曲面」を考える。
この時「電場が貫く閉曲面の面積$S$」と「電場$E$」の積が
「閉曲面内部の電荷の総和$Q$」を定数$\epsilon_0$で割ったものに等しい。
これに従い、先ほどの図において、
電場が垂直に貫くような閉曲面
を考えましょう。
今回の場合、そのような適切な閉曲面は
電荷を中心とした「球面」です。
上の図では2次元なので円になっていますが、
立体的には球面であることに注意してください。
そして、ガウスの法則から
閉曲面の面積$S$と電場$E$の積が
閉曲面内の電荷の総和$Q$を
定数$\epsilon_0$で割ったものに等しい
のでした。
球面の面積$S$はその半径を$r$とすると、
$$\large S = 4\pi r^2$$
また、点電荷を考えているので電荷の総和$Q$は
$$\large Q = q$$
と書けることに注意すると、
ガウスの法則から
$$\large 4\pi r^2 \cdot E = \frac{q}{\epsilon_0}$$
（(閉曲面の面積)×(電場)＝(電荷の総和)/$\epsilon_0$）
という式を得ることができます。
この式を変形して「$E=$」の形に直すと、最終的に
$$\large E = \frac{q}{4\pi\epsilon_0r^2}$$
という点電荷が作る電場の式を得ることができます。
そしてこれは、クーロンの法則から得られる
点電荷が作る電場の式にちゃんと一致しています（！！！！）
具体例２：平面が作る電場
次に、下の図のような
平面上に敷き詰められた電荷
が作る電場を考えていきます。
今の場合、これが無限に広がっていると考えてください。
つまり、今から考えるのは
無限に広い平面に敷き詰められた
電荷が作る電場
です。
これを考えることは、
コンデンサーの
片方の極板が作る電場
を考えることに相当します。
（コンデンサーの極板間の電場ではないことに注意）
ステップ１：平面が作る電場の向きを考える
平面状に敷き詰められた電荷のうち
2つの隣り合った電荷に注目します。
各々の電荷は先ほど解説したように
四方八方向かって電場を作ります。
その結果、次図のように、
隣り合う電荷が作る電場のうち、
横向きの成分は打ち消し合い、
上向き、もしくは
下向きの電場しか残らない
という事が起こります。
そして、このようなことが
平面上の至るところで起こる結果、
平面全体が作る電場の向きというのは
このように、
平面に対して垂直
になります。
電場の向きが平面に対して垂直になることがわかったので
次にガウスの法則を実際に適用していきます。
ステップ２：ガウスの法則を適用してみる
再度、ガウスの法則を載せます。
電場というのは電荷があれば
四方八方に向けて発生し、その向きは
負電荷ならば吸い込むように
正電荷ならば湧き出すように
発生する。
電荷が作る電場が垂直に貫くような
「電荷を囲む閉曲面」を考える。
この時「電場が貫く閉曲面の面積$S$」と「電場$E$」の積が
「閉曲面内部の電荷の総和$Q$」を定数$\epsilon_0$で割ったものに等しい。
先ほど考えたように、平面のが作る電場の方向は
このように平面に対して垂直です。
そのため「平面の作る電場が垂直に貫く閉曲面」
というのは、次の図ような
直方体の表面
になります。
電場は上か下にしか出ていないので、
直方体の側面を貫いている電場は存在しないことに注意して下さい。
この直方体の上面と下面の面積を$S$と書きます。
また、この直方体で囲まれた平面上の電荷の総和を$Q$とします。
すると、今、電場が垂直に貫く面積は
上面と底面の面積を合わせた$2S$になることに注意して
ガウスの法則から
$$\large 2S\cdot E = \frac{Q}{\epsilon_0}$$
（(電場が貫く閉曲面の面積)×(電場) = (閉曲面内の電荷の総和)/$\epsilon_0$)）
ここからさらに
電場の式（「$E=$」）の形に変形して、
$$\large E = \frac{Q}{2S\epsilon_0}$$
という平面が作る電場の式を得ることができます。
この式には
平面からの距離
という変数が含まれていない
ということに注目してください。
つまり、平面が作る電場の大きさというのは、
平面からどれだけ離れようと変わりません。
（これは”無限に広い平面”という非現実的な状況を考えたために起こります）
“簡易的”なガウスの法則であることに注意
今回解説してきたガウスの法則というのは
厳密なガウスの法則ではなく、
高校生向けの
簡易的なガウスの法則
であることに注意してください。
このガウスの法則というのは
大学で物理を習わない限り出会うことはありません。
そのため、高校物理でやる「必要」はないです。
しかしこれをわかっておくと、
電場に対する解像度がより高くなり、
電磁気の分野で何かと役に立つので、
今回解説した内容程度は頭に入れておくとおすすめです。
- ①電場が垂直に貫くような閉曲面を考える
- ②その内部の電荷の総和を考える
- ③（電場）×（閉曲面の面積）=（電荷の総和）/$\epsilon_0$
という式を変形することで電場を求めることができた！ - 以上がガウスの法則の概要。
- 点電荷が作る電場の式：$E = \frac{q}{4\pi \epsilon_0 r^2}$
- 平面が作る電場の式：$E = \frac{Q}{2S\epsilon_0}$
- 電場の対する解像度を上げても損はないから
積極的にガウスの法則を取り入れて行こう！ - （より厳密なガウスの法則は大学でやるよ！）
当サイトでは、微積物理を学ぶ際のハードルとされる「数学的難解さ」を極限まで排除し、
物理が一気にわかって成績上がることを目指して作られた「真・微積物理速習テキスト」を販売しています！
(
・数学編では必要最低限の数学を。
・力学編では無料公開版には収録できなかった内容を。
・電磁気編では多くの受験生がつまづきやすい箇所を重点的に解説。
(
(物理の本質をよりわかりやすく、より速く、サクサク学べる秘伝のテキストです！
さらに、志望校合格に2歩も3歩も近づける充実の特典もあります！
・力学、電磁気学を微積物理を使って学びたいという意欲のある方
・学びたい気持ちはあるが、理解できるか自信のない方
・物理を得意になりたい方
(
におすすめです！
この機会にぜひ検討してみてください！
力学・電磁気学を微積を使って学べる完全版テキストはこちらから詳細についてこちらから
無料体験版をLINE@で配布しています！
求む！今のうちにライバルと差をつけたい新受験生！
皆さんの「ここを教えてほしい」を募集しています！
高校物理に関して「ここがわからない」「この問題の解説が理解できない」などなど、質問を募集しています！
気軽に質問してください！
質問内容に関しては記事として回答させていただきます！
⚠️質問の回答は先着順で回答していくため、質問から回答までの期間が長くなることがあります。あらかじめご了承ください。
何を言っているのか
さっぱりわからない