あの「微積物理」を無料で学べます！！
Contents
問題設定
今回は
3枚の極板からなる
コンデンサー
を使った問題について解説していきます！
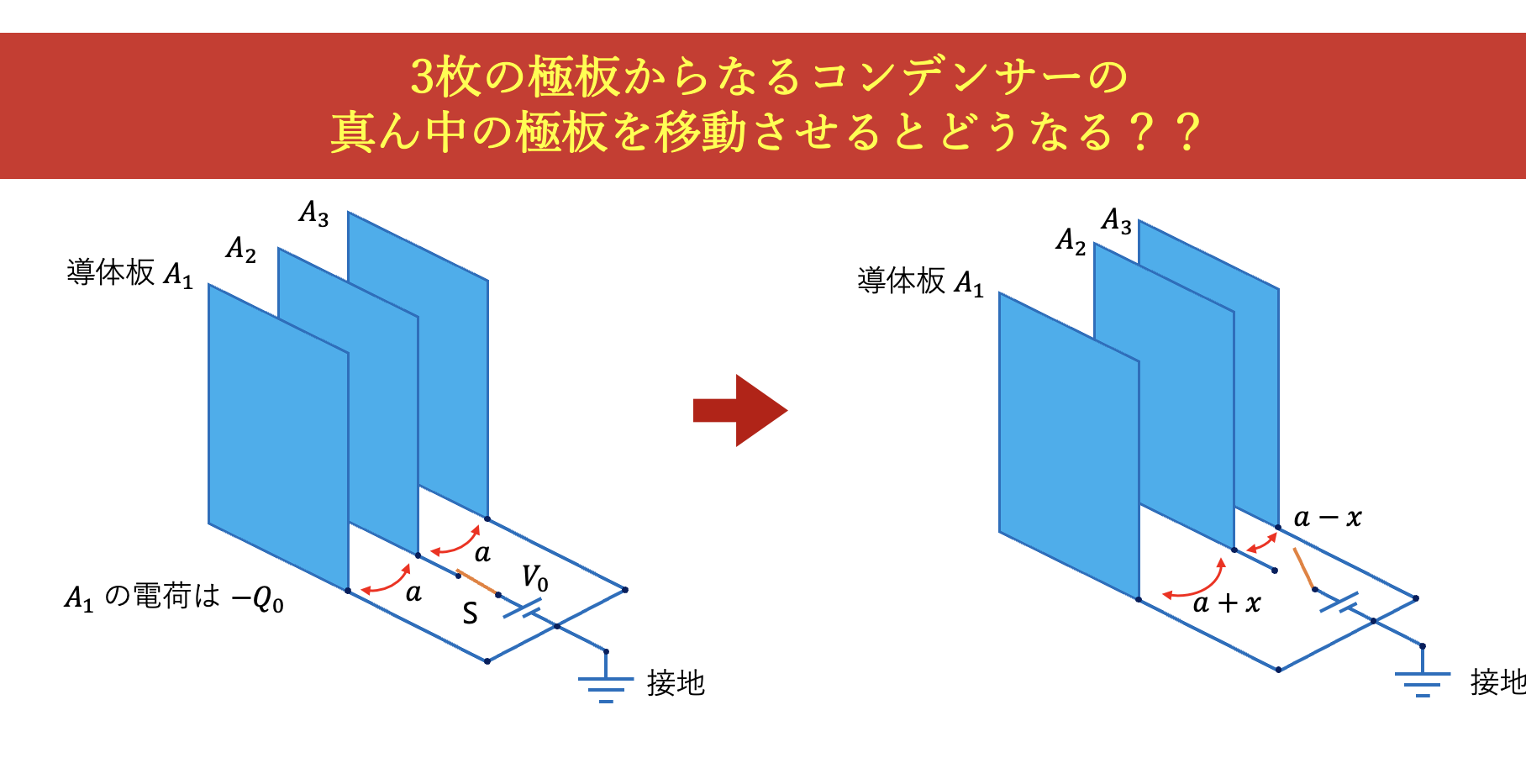
図1のように面積の等しい3枚の導体板$A_1, A_2, A_3$を平行に置き
間隔が共に$a$となるようにして固定した。
図1
$A_1, A_3$を接地し、スイッチSを閉じて$A_2$の電位を$V_0$にすると$A_1$の電荷は$-Q_0$となった。
図1における$A_1, A_2$間の電気容量を$C$として次の問いに答えよ。
- （1）$A_2$の電荷を求めよ。
次にスイッチを切り、図2のように$A_2$を$A_3$の方へ$x$だけ動かした。$(x<a)$
図2
- （2）このとき、$A_2$を求めよ。
- （3）$A_1$の電荷を求めよ。
小問それぞれについて、以下で詳しく解説していきます！
移動させる前の電荷
それではまず、(1)を解くために必要な考え方を解説していきます。
コンデンサーの電気容量$C$というのは
具体的に
$$\large C=\frac{\epsilon_0 S}{d}$$
（$d$：極板間の距離、$S$：極板の面積、$\epsilon_0$：真空の誘電率）
と書くことができ、この式から明らかなように
コンデンサーの電気容量というのは
極板間の距離
と
極板の面積
によって決まります。
今の場合、3枚とも極板の面積は等しく、
極板を移動させる前では$A_1$と$A_2$、
$A_2$と$A_3$の極板の距離は同じく$a$です。
そのため、$A_1$と$A_2$間の電気容量と
$A_2$と$A_3$の電気容量は同じになります。
また、今問題にしている回路は
このように、
2つのコンデンサーが
並列につながっている
とみなすことができるので、
極板間の電位差も同じになります。
(1)を解く場合にはこのことに十分気をつけるようにしてください。
問題(1)を解く
それでは問題を解いていきましょう。
コンデンサーの極板に溜まる電荷$Q$は
$$\large Q= CV$$
で求めることができるので、電気容量$C$と
電位差$V$が等しい$A_1$と$A_2$、$A_2$と$A_3$の
2つの極版間では同じ量の電荷が溜まることになります。
今の場合、極板$A_1$に電荷が
$-Q_0$だけ溜まっていることから
極板$A_3$に溜まっている電荷も$-Q_0$だとわかります。
そして、それらと
符号が反対で同じ量の
電荷が極板$A_2$に溜まる
ことになるので、
(1)で問われている極板$A_2$の電荷は
$$\Large +2Q_0$$
だとわかり、これが答えになります。
ちなみに今の場合、$A_1$と$A_2$、
$A_2$と$A_3$によって作られるコンデンサーの電気容量$C_0$は
$$\large C_0 = \frac{Q_0}{V_0}$$
と書けます。
極板を移動させた後の状態について
それでは次に、(2)(3)を解くために必要な考え方について解説していきます。
今、問題を解く上で注意すべきことは以下の3つです。
注意事項その①：電荷の保存
1つ目は
孤立部分の電荷は
突然消えたり増えたりしない
ということです。
スイッチを切ったので、それまで$A_2$に
溜まっていた電荷$+2Q_0$はどこにも移動することはできません。
つまり、$A_2$の電荷が突然消えたり、
突然増えたりすることもありません。
注意事項その②：コンデンサーの電気容量の式
問題(1)の方でも言いましたが、
コンデンサーの電気容量は
極板間の距離$d$と
極板の面積$S$によって
$$\Large C=\frac{\epsilon_0 S}{d}$$
のように決定される
ということに注意するようにしてください。
この関係に注意すれば
移動後の電気容量の大きさ、また、
極板間の移動後の電気容量が
移動前の電気容量に比べて何倍になったか
をすぐに求めることができます。
注意事項③：回路は並列回路になっている
これも問題(1)で言いましたが、
今考えている回路では
このように、コンデンサーが並列につながっているとみなせ、そのために
$A_1$と$A_2$、$A_2$と$A_3$の
極板間の電位差は同じ
になります。（並列回路の基礎）
極板間の距離が変化しても
電位差は同じであることに注意してください。
以上のことに気をつけて問題を解いていきましょう。
問題(2)(3)を解く
再度、問題と図を示します。
スイッチを切り、図2のように$A_2$を$A_3$の方へ$x$だけ動かした。$(x<a)$
図2
- （2）このとき、$A_2$を求めよ。
- （3）$A_1$の電荷を求めよ。
$A_2$の電圧を求めるために今使えそうなのは
コンデンサーの関係式
$$\large Q = CV$$
です。
今考えている回路は
このように
並列回路だとみなせる
ので、$A_1$と$A_2$、$A_2$と$A_3$の極板によって作られる
2つのコンデンサーの電位差は同じです。
そして、この電位差が求めたい$A_2$の電位になります。
この電位差をどうやって求めるか、
ですがここで
$A_2$における電荷の保存の関係式
が使えます。
というのも、電荷についての関係式が得られれば
コンデンサーの関係式：
$$\Large Q = CV $$
を用いることで
電荷の式から
電位差（電位）の関係式へ
持ち込める
からです。
電荷の保存の式を立てる
そこで、移動後の極板$A_2$において、
極板$A_1$側に溜まっている電荷を$Q_1$、
極板$A_3$側に溜まっている電化を$Q_3$で書くことにします。
移動前の$A_2$の電荷は(1)より$+2Q$であり
スイッチを切り、電荷がどこにも移動できなくなった状態で
極板を動かしても孤立した$A_2$では電荷が移動できず保存するので、
$$\Large Q_1+Q_2=2Q_0$$
（（移動後の電荷の合計）＝（移動前の電荷の合計））
という式を得ることができます。
電荷の式を電位差の式に書き直す
ここで、移動後の極板$A_1$と$A_2$間、
$A_2$と$A_3$間の電気容量を（電荷と同様に）$C_1$、$C_2$と書き、
求めたい電位を$V$で書きます。
すると、コンデンサーの関係式から
$$\Large Q_1 = C_1V$$
$$\Large Q_2 = C_2V$$
と書くことができるので、これを
先ほどの電荷の保存を意味する式：
$$\large Q_1+Q_2=2Q_0$$
に代入して、
$$\Large C_1V+C_2V=2Q_0$$
を得ることができます。
念の為言っておくと、この式において
電位$V$が「求めたい量」であり、
$Q_0$は「既にわかっている量」、
$C_1$、$C_2$は「まだわかっていない量」です。
この2つの電気容量がわかれば「$V=$」
の形に式を変形することで、求めたい$V$を得ることできます。
移動後の電気容量の表式を求める
この2つの電気容量の表式を求めるために
コンデンサーの電気容量が
$$\Large C = \frac{\epsilon_0 S}{d}$$
（$d$：極板の暑さ、$S$：断面積）
という式でかけたことを思い出してください。
この式から、極板の断面積を$S$とおくと、
極板間の距離が、
このようになっていることに気をつけて、
$$\large C_1 = \frac{\epsilon_0 S}{a+x}$$
$$\large C_2 = \frac{\epsilon_0 S}{a-x}$$
と書くことができ、これらをさらに変形することにより、
$$\large C_1 = \frac{\epsilon_0 S}{a+x}=\frac{\epsilon_0 S}{a}\cdot \frac{a}{a+x}$$
$$\large C_2 = \frac{\epsilon_0 S}{a-x}=\frac{\epsilon_0 S}{a}\cdot\frac{a}{a-x}$$
と書けます。
ここで、
$$\Large \frac{\epsilon_0 S}{a}$$
の部分に注目してください。
これは、
極板間の距離が
$a$である場合の電気容量
を意味しており、これはつまり
極板を移動させる前の電気容量
のことです。
問題(1)の最後で述べたように、
極板を移動させる前の電気容量は
$C= \frac{Q_0}{V_0}$と書けるので、
$$\Large \frac{\epsilon_0S}{a} = \frac{Q_0}{V_0}$$
という関係を得ることができます。
これをC1とC2を求める先ほどの式に代入して、
$$\Large C_1 =\frac{Q_0}{V_0}\cdot \frac{a}{a+x}$$
$$\Large C_2 =\frac{Q_0}{V_0}\cdot\frac{a}{a-x}$$
が得られます。
この電気容量の式を$(C_1+C_2)V=2Q_0$ に代入して、
$$\large \Big(\frac{Q_0}{V_0}\cdot \frac{a}{a+x}+\frac{Q_0}{V_0}\cdot \frac{a}{a-x}\Big)V=2Q_0$$
これで、わからない量が$V$だけの式が得られたので、
上式を適切に変形し「$V$=」の式にしてきます。
すると、
$$\large \frac{Q_0V}{V_0} \Big(\frac{a}{a+x}+\frac{a}{a-x}\Big)= 2Q_0$$
両辺をQ_0で割り、()の中身を整理して、
$$\large \frac{V}{V_0} \Big(\frac{a(a-x)+a(a+x)}{(a+x)(a-x))}\Big)= 2$$
最終的に
$$\Large V = \frac{a^2-x^2}{a^2}V_0$$
という表式を得ることができます。
これが(2)の答えです。
$A_1$の電荷を求める：問題(3)
最後に、$A_1$の電荷を求めていきます。
(2)を考える過程で求めたように、
極板$A_1$と$A_2$で作られる
コンデンサーの電気容量$C_1$の表式は
$$\large C_1 =\frac{Q_0}{V_0}\cdot \frac{a}{a+x}$$
と書けます。
これと(2)で求めた電圧Vを使うことにより
$A_1$の電荷$Q_1$は、その符号に気をつけて
$$\large Q_1 = -C_1V = -\frac{Q_0}{V_0}\cdot \frac{a}{a+x}\cdot \frac{a^2-x^2}{a^2}V_0$$
最終的に
$$\Large Q_1 = -\frac{a-x}{a}Q_0$$
と書くことができます。
これが(3)の答えです。
$Q_1 = -C_1V$という式で、
なぜ負符号がつくの？
と疑問に思ったかもしれませんが、
これは、コンデンサーでは
同じ大きさで符号が逆の電荷が
2つの極板に溜まる
ためです。
今の場合、$A_1$と$A_2$で作られる
コンデンサーに注目すると、
$A_2$の方に正の電荷が溜まっているため、
$A_1$の方には「負電荷」が
$A_2$の正電荷と同じだけ
溜まることになります。
コンデンサーの関係式：$Q = CV$を使う時、この$Q$というのが
2つ極板それぞれに溜まる
電荷の”大きさ”を表している
（符号までは考慮してない）
ということに十分気をつけてください。
まとめ
それでは今回のまとめです。
- コンデンサーの電気容量は
「極板間の距離」と「極板の面積」によってのみ決まる！ - 極板間の距離が変わっても、並列回路なら電圧は変わらない！
- 孤立した部分では電荷は突然消えたり増えたりしない！
- 極板の距離が変わっても$Q = CV$という関係式を用いて冷静に処理する！
- コンデンサーの関係式：$Q = CV$の$Q$はあくまで電荷の”大きさ”であり、
符号は自分で別に考慮する必要があることに注意する！
あの「微積物理」を無料で学べます！！
皆さんの「ここを教えてほしい」を募集しています！
高校物理に関して
「こんなことを教えて欲しい」
「この問題をわかりやすく解説して欲しい！」
「勉強のコツを知りたい！」
などなど、質問を募集しています！
気軽に質問してください！無料です！
質問内容に関しては記事として回答させていただきます！
⚠️質問の回答は先着順で回答していくため、質問から回答までの期間が長くなることがあります。あらかじめご了承ください。
コメントを残す