斜方投射の問題を解けるようになるために！「斜方投射の公式」の求め方まとめ！

斜方投射の公式一覧

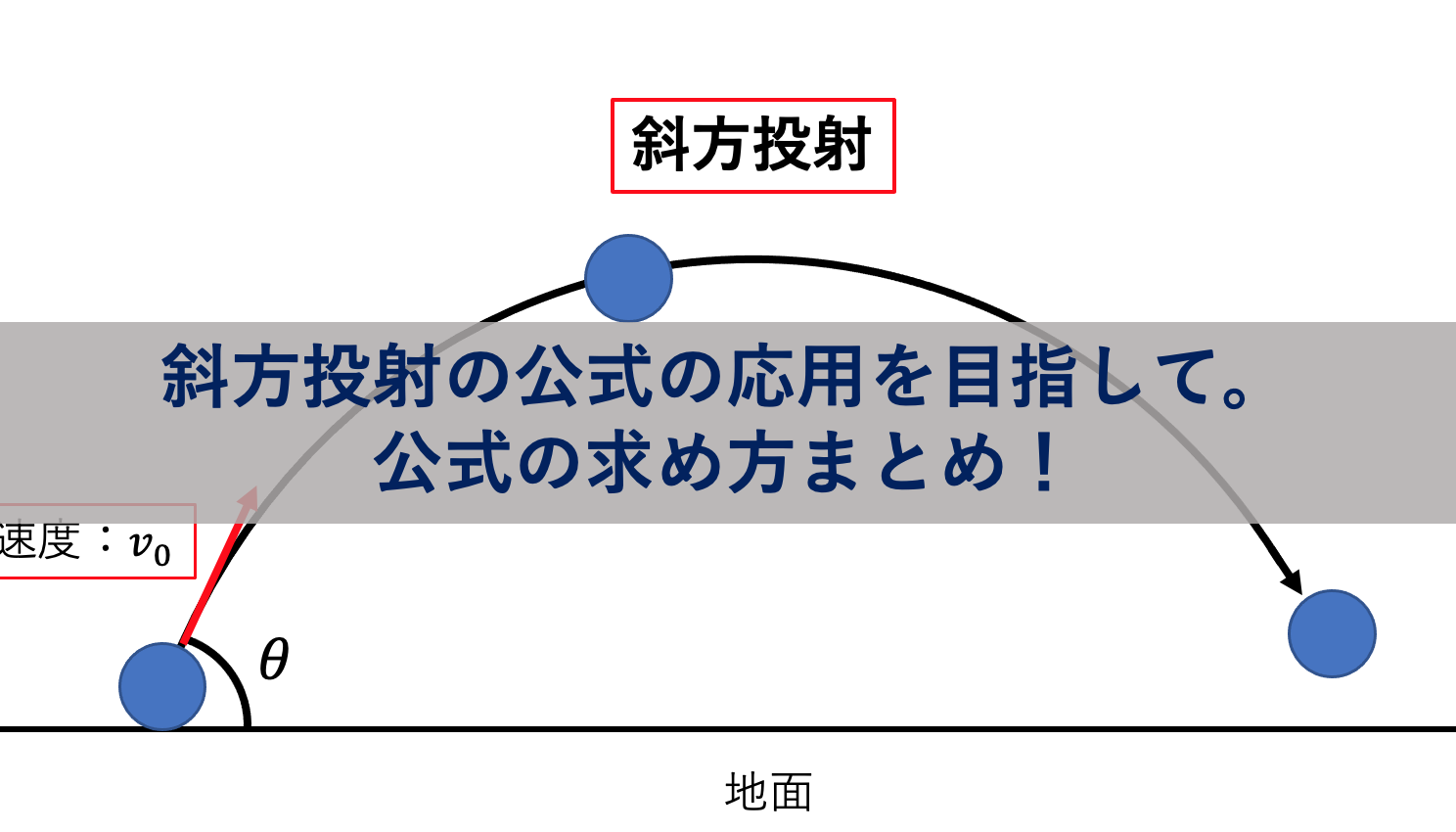
次のような

斜方投射

の運動を考えます。

この時、斜方投射の公式として
次のようなものがあります。

とてもたくさんありますが
これらは

全く覚える必要がない

ので安心してください。

逆に、決して
丸暗記だけはしないように
しましょう。

これらは全て自力で求めることが
できるようになってください！

斜方投射の公式の求めるために

先程の公式たちを求めるにあたり
これ以降は

鉛直投げ上げ運動
の知識を前提として

進めていきます。

なのでその点があやふやな人は
以下で復習しておきましょう。

あわせて読みたい
鉛直投げ上げ運動に
自信がない方はこちら

自由落下・鉛直投げ上げ・鉛直投げ下ろしの公式とその導出まとめ！

2021年4月22日

物体の運動は2つの方向に分割せよ

上にあげた図に
とりあえず、いつも通り
物体に働く力を書き足します。

今働くのは重力だけなので
この物体の質量を$m$とすると

となります。

斜方投射を考える時に
大事になるのは

各方向に運動を
分解すること

です。

逆に、斜方投射という運動は

分解した運動の
組み合わせ

で表現できます。

ということで縦軸と横軸へ
物体の運動を分解してみましょう。

すると次のようになります。

縦軸の運動：鉛直投げ上げ

それではまず
縦軸へ分解された運動
について考えてみましょう。

この運動は重力が働く状態で
真上に投げ上げられてているので
これはまさに

鉛直投げ上げ運動

を表しています。

また、この場合その初速度は
斜方投射の初速度が$v_0$だったので

$$\large v_0\sin\theta$$

となります。

横軸の運動：等速直線運動

次に斜方投射のうち
横軸へ分解された運動
について考えてみましょう。

この運動では

力が全く働いていない
かつ
初速度がある

ということに注目してください。

つまりこの物体は
慣性の法則により、

等速直線運動

をします。

そしてその初速度は
先と同様に、斜方投射の
初速度が$v_0$であるので

$$\large v_0\cos\theta$$

となります。

公式の具体的な求め方

さて、斜方投射が

鉛直投げ上げ
と
等速直線運動

に分解できることがわかり
それらの初速度がわかったなら
あとはもう簡単です。

知ってる公式を組み合わせるだけで
全て求めることができます。

運動の軌跡の求め方

運動の軌跡を求めるとはつまり

座標$x$と座標$y$の
間に成立する式

を求めることを意味します。

そこで次の
鉛直投げ上げ運動と等速直線運動における
位置（$y$と$x$）を表す2つの式を用意します。

$$y=v_0\sin\theta\cdot t-\frac{1}{2}gt^2$$

$$x=v_0\cos\theta\cdot t$$

そして等速直線運動の式を
次のように$t$についての式
に変形します。

$$t=\frac{x}{v_0\cos\theta}$$

今度はこれを
鉛直投げ上げ運動の公式
に代入します。

そのようにすると、次のように
$y$の式から$t$が消えて、
$x$と$y$の式になります。

\begin{align}
y&=v_0\sin\theta \cdot \frac{x}{v_0\cos\theta}-\frac{1}{2}g\Big(\frac{x}{v_0\cos\theta}\Big)^2\\
\\
&=x\frac{\sin\theta}{\cos\theta}-\frac{g}{2v_0^2\cos^2\theta}x^2\\
\\
&=-\frac{g}{2v_0^2\cos^2\theta}x^2+x\tan\theta
\end{align}

最終的に

$$\large y=-\frac{g}{2v_0^2\cos^2\theta}x^2+x\tan\theta$$

が得られます。

これが軌跡の式であり
この式は何を隠そう

2次関数

になっており、これを実際に
プロットしてみると

となり、確かに斜方投射を
表していそうだと
わかると思います。
（上図では$y=0$が地面に相当）

最高点の高さ

次に最高点の高さについてです。

今の場合「高さ」
を知りたいので

縦軸の運動

のみを考えればすみます。

つまり

横軸の運動は
無視できる

と言えます。

そして縦軸の運動とは
鉛直投げ上げ運動であり
この運動において
高さが最大になるのは

速度が0になった時

でした。（復習）

なので鉛直投げ上げ運動の
次の公式

$$v^2-v_0^2=-2gy$$

に$v=0$と
初速度$v_0\sin\theta$を代入して

\begin{align}
0-(v_0\sin\theta)^2&=-2gy\\
\\
v_0^2\sin^2\theta&=2gy\\
\\
\large y&=\large \frac{v_0^2\sin^2\theta}{2g}
\end{align}

が得られ、これが
今求めたい最大の高さとなります。

最高点に達するまでの時間

最高点に達するまでの時間を
求めたい場合も先ほどと同様に
横方向の運動は無関係なので無視できます。

つまり考えるべきは

鉛直投げ上げ運動において
最高点に達するまでの時間

になります。

これは鉛直投げ上げ運動の
速度に関する次の公式

$$v=v_0-gt$$

に$v=0$と初速度を
代入することで得られます。
（なぜなら最高点で縦軸方向の速度は0となるから）

よって結局

$$\large t=\frac{v_0\sin\theta}{g}$$

が得られ、これが
最高点に達するまでの時間
になります。

最高点に達した時の水平距離

では
最高点に達したの時の水平距離
はどれくらいでしょうか。

まず考えなければいけないのが

最高点に達するまでの
経過時間

です。

これがわかれば、水平方向には
等速直線運動
をしているため水平距離は

$$\large x=v_0\cos\theta \cdot t$$

で表されるので
この式の時間$t$に
その経過時間を代入することで
求めることができます。

そしてその経過時間、つまり
最高点に達するまでの時間
は、上の節から

$$t=\frac{v_0\sin\theta}{g}$$

で与えられるのでした。

あとはこれを等速直線運動の式に代入するだけです。

\begin{align}
x&=v_0\cos\theta \cdot \frac{v_0\sin\theta}{g}\\
\\
&=\frac{v_0^2\sin\theta\cos\theta}{g}\\
\\
&=\frac{v_0^2\sin2\theta}{2g}
(倍角の公式)
\end{align}

このようにして結局

$$\large x=\frac{v_0^2\sin2\theta}{2g}$$

が得られ、これが
最高点に達した時の水平距離
になります。

落下するまでに要する時間

物体が投射されて
次に地面に落下するまでに要する時間は
鉛直投げ上げ運動において

物体が落ちて
来るまでの時間

に等しいです。

それは高さ$y$を表す
次の式

$$y=v_0\sin\theta\cdot t-\frac{1}{2}gt^2$$

に$y=0$を代入することで求まります。
（なぜなら物体が落ちて来る＝原点（$y=0$）に戻って来る、から）

もしくはその速度を表す次の式

$$v=v_0\sin\theta-gt$$

に$v=-v_0\sin\theta$を代入するか
で求まります。
（なぜなら物体が原点に戻って来る際
大きさが同じで逆向きの速度を持っているから）

このいずれかを用いると
最終的に求める時間は

$$\large t=\frac{2v_0\sin\theta}{g}$$

となります。

これが
落下するまでに要する時間
です。

水平到達距離

水平到達距離とは
次で表される距離を表します。

ではこれを求めていきましょう。

水平到達距離は
投げ出してから
落下するまでに要する時間を
横軸の運動である
等速直線運動の次の公式

$$x=v_0\cos\theta \cdot  t$$

に代入することによって
求めることができます。

そして落下するまでに要する時間は
前の節から

$$t=\frac{2v_0\sin\theta}{g}$$

で与えれらるので、これを代入して

\begin{align}
x&=v_0\cos\theta \cdot  \frac{2v_0\sin\theta}{g}\\
\\
&=\frac{2v_0^2\sin\theta\cos\theta}{g}\\
\\
&=\frac{v_0^2\sin2\theta}{g}
\end{align}

最終的に

$$\large x=\frac{v_0^2\sin2\theta}{g}$$

が得られ、これが
水平到達距離になります。

水平到達距離を最大にする角度

前の節で求めた次式で表される
水平到達距離において
水平到達距離を最大にする角度を考えます。

$$\large x=\frac{v_0^2\sin2\theta}{g}$$

この式において

$\sin2\theta$がどんな値の時
$x$は最大になるか

というのが今の場合考えなくてはいけないことです。

上式から、明らかに
$\sin2\theta$が最大の時
$x$も最大になります。

そして$\sin2\theta$の
最大値は1です。

そのため

$$\sin2\theta=1$$

である角度が求める角度になります。

そしてこの角度は明らかに

$$\theta=\frac{\pi}{4}=45°$$

です。

これが
水平到達距離を最大にする角度
になります。

まとめ

それでは今回のまとめです。