運動方程式とは
単刀直入に運動方程式とは
次の式で表される方程式のことです。
$$\Large m\frac{d^{2}x}{dt^{2}}=F$$
$$\large m:質量 , F:力$$
$$\Large \frac{d^{2}x}{dt^{2}}$$
は加速度を表しますが
この点がよくわからない方は
以下を参照してください。
そしてこれは普通の高校物理だと
次のように表されます。
$$\Large ma=F $$
$$\large a:加速度$$
これは
力が働くと
加速度が生まれること
を意味しており、
全ての物体はこの式に従い運動します。
そして微積物理においてこの式は
見てわかるように
微分方程式
です。
運動方程式の右辺は
力
運動方程式の左辺は
質量と加速度の積
という全く違ったものが
「=」でつながっていることが
ポイントです。
この式において質量$m$というのは
さほど重要ではありません。
ただ「おまけでついてるもの」
ぐらいの認識でいてください。
重要なのは加速度$a$の方です。
つまりこの式は
加速度と力という
全く違ったものを繋ぐ等式
ということです。
ここで次のように右辺を左辺に
または、左辺を右辺に移項した
次のような式を考えてください。
$$\Large m\frac{d^{2}x}{dt^{2}}-F=0$$
$$\Large 0=F-m\frac{d^{2}x}{dt^{2}}$$
多くの人はこれらの式を
運動方程式と同じもの
だとみなしがちです。
しかしこれらは運動方程式とは
全く違います。
もちろん数式としては
同じでしょう。
しかし物理としては
全く違います。
物理における運動方程式では
(左右どちらの辺にどちらを
書いてもいいですが)必ず
片方は加速度のみ
片方は力のみ
を書く必要があります。
なぜかというと
それが運動方程式であり
それ以外は運動方程式ではないから
です。
このあたりを誤解し
後々混乱する人がたくさんいるので
(特に「慣性力」を考える場合)
「力」と「加速度」は
同じ辺に書いてはいけない
ということは肝に銘じておいてください。
運動方程式の立て方
次に
運動方程式の立て方
を説明していきます。
これも具体例を考える方が早いと思うので
以下のような場合を考えます。

まず自分の考えやすいように
座標を設定し
「正の方向」を決めます。
今回は次のように座標を設定し
右方向を正としましょう。

物理では自分の好きなように
好きな座標と正の方向
を選ぶことができます。
そうするとこの時
正方向に力が働いている
ので運動方程式は次のようになります。
$$\Large m\frac{d^{2}x}{dt^{2}}=F$$
以上のようにして運動方程式を
立てることができます。
さらにより良く理解してもらうために
別の場合も考え見ましょう。
考えるのは先ほどと同様の物体です。

しかし、今回は先ほどとは違って
逆向きの座標
を取ることにします。

するとこの場合
正方向も
逆になっている
ので、この時の力は
負の方向に働く力
です。
その結果運動方程式は
次のようになります。
$$\Large \frac{d^{2}x}{dt^{2}}=-F$$
このように
自分でどの向きを正とするかによって
力の符号は変わるので注意しましょう。
ただし
実際起こっている
事象自体は変わらない
ので注意してください。
注意:加速度の符号は変わらない
上で説明したように
座標の取り方・向きの取り方
によって力の符号は変わります。
この際加速度について
$$\Large m\frac{d^{2}x}{dt^{2}}→m(-\frac{d^{2}x}{dt^2})$$
のように
加速度の符号を
変えてしまう間違い
が起こりがちです。
しかし
座標の取り方・向きの取り方
で符号が変わるのは力だけ
であることに注意してください。
ここで加速度も符号を変えてしまうと
上の場合において
図を見れば明らかなように
負の方向に加速していく
のにもかかわらず
運動方程式では
\begin{equation}
\begin{split}
\Large m(-\frac{d^{2}x}{dt^{2}})&=\Large -F \\
\\
\Large m\frac{d^{2}x}{dt^{2}}&=\Large F
\end{split}
\end{equation}
となり、
正方向に力が働く場合と同じ
になってしまいます。
しかしこれは
負の方向に力が働いているので
明らかにおかしいです。
なので
座標の取り方・向きの取り方
で符号が変わるのは力だけ
であることは忘れないようにしましょう。
そしてこれはつまり
運動方程式の
左辺はいつも同じで
$\Large m\frac{d^{2}x}{dt^{2}}$
であるとも言えます。
運動方程式の右辺については
何も余計な心配を
することなしに
つまり
脳死状態で
ただ
$$\Large m\frac{d^{2}x}{dt^{2}}$$
と書けばいいわけです。
無駄な間違いをしないために
気をつけましょう。
全ては運動方程式から始まる
微積物理では
全ては運動方程式から
始まります。
普通の高校物理では
エネルギー保存の式
力積の式などなど
いろんな公式と
その使い方の暗記
が必要でした。
しかし微積物理においては
全ては運動方程式から
結果として
導かれます。
つまり微積物理では
運動方程式が
唯一暗記すべき式
なわけです。
この点で微積物理はとても便利です。
なので物理の問題に取り組む際には
とにかく最初は
運動方程式!
を徹底してください。
普段の物理では
最初にやるべきことは様々なため
そこで間違いが生じがちです。
しかし微積物理では
最初に運動方程式さえ書けば
あとは自然に求まります。
そのため
最初に間違いが
生じる要素がない
という利点もあります。
まだこの利点をあまり
感じられてないかもしれませんが
これからさらにたくさんの感動を
味わうと思うので期待しておいてください。



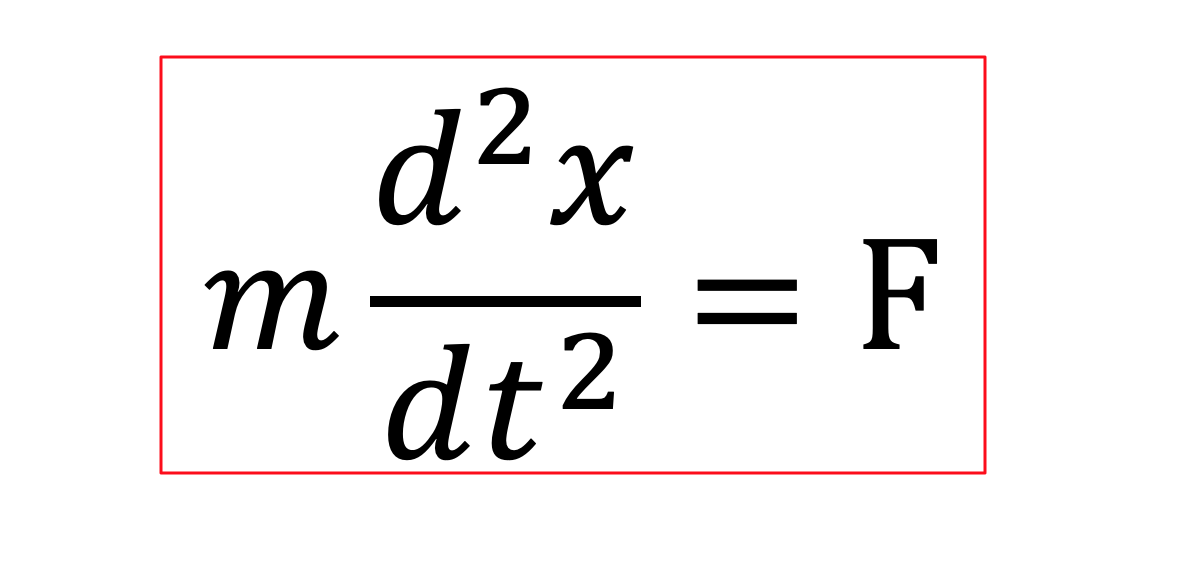













コメントを残す