Contents
微分の概説
ここからは微積物理を勉強する上で
とても大事な数学である
微分
について解説していきます。
難しそうだと身構えるかもしれませんが
初学者にもわかるように心がけたので
難しく考え過ぎないように!
微分はとてもシンプルです。
それではまず次のように
とある関数$y=f(x)$のグラフを考えます。

そしてどこでもいいので
座標がそれぞれ
$(x_a, f(x_a))$と$(x_b, f(x_b))$
である点A、点Bを定め
次のように直線で繋ぎます。

この直線ABの
傾きまたは平均変化率は
$$\Large \frac{y座標の変化}{x座標の変化}$$
で与えられるので
次のように書くことができます。
$$\Large 傾き=\frac{f(x_b)-f(x_a)}{x_b-x_a}$$
ではこの適当にとった
点Bを点Aに
どんどん近づけていく
と先ほどのような
直線はどうなるでしょうか。
これは図に示すと
次のようになります。






上の図のように
その直線ABはだんだん
関数$f(x)$の
点Aにおける接線
に近づいていきます。
ではここからさらに
点Bを限りになく
点Aに近づけていく
ようにすると直線はどうなるでしょうか。
お察しの通り、最終的には
点Aにおける接線
になります。

ではこの時
ABの傾きの値
はどうなっていくでしょうか。
先ほど示したようにその値は
$$\Large 傾き=\frac{f(x_b)-f(x_a)}{x_b-x_a}$$
で与えられます。
そしてこの時
点Bを点Aに限りなく近づける
というのは上の式において
$\large x_b$を$\large x_a$にどんどん近づけることになります。
この操作は数式で
$$\large \lim_{x_b \to x_a}\frac{f(x_b)-f(x_a)}{x_b-x_a}$$
と書かれます。
この$\lim$は
何かの数を無限に
何かに近づける
ことを意味します。
これは
値を代入するわけではない
ので注意してください。
そして上の式はさらに
$\Delta x$と$\Delta f$を
$$\Large \Delta x= x_b-x_a$$
$$\Large \Delta f= f(x_b)-f(x_a)$$
で定義すると
$$(点Aでの傾き)=\Large \lim_{\Delta x \to 0}\frac{\Delta f}{\Delta x}$$
とかけます。
そしてこのような
ある1点での
傾きを求める操作
のことを
微分
と言います。
微分はさらに
次のように表現されます。
$$\Large \frac{df}{dx} = \lim_{\Delta x \to 0}\frac{\Delta f}{\Delta x}$$
上の式は「d」を「微小」を意味するものだと考え
$f(x)$の微小な変化$df$を
$x$の微小な変化$dx$で
割っている式
というような覚え方を
すると良いです。
そしてこのような覚え方をすれば
これは一般的な
直線の傾きの求め方である
$$\Large \frac{y座標の変化}{x座標の変化}$$
と一致します。
また微分は
$$\Large \frac{df}{dx}= \frac{d}{dx}f(x) = f'(x)$$
のように書く場合もあり
どちらの場合にしてもこの操作を
$f(x)$を$x$で微分する
と言います。
以上が微分の説明になります。
簡単だったでしょ?
疑問があれば
遠慮なく質問してください!
一般的な微分の公式
次に
一般的な微分の公式
を以下に列挙します。
もちろん数学的な証明はできますが
それは物理への応用には必要ありません。
物理で微積を使う場合には以下の式は
結局「覚える」ほど使うので
最初から以下の式は
なんでかわかんないけど
とりあえずこいつらは成り立つんだな
と了解してしまって覚える方が得策です。
数学の勉強を進めていけばいずれ
以下の公式の証明を
勉強することになります。
定数の微分
$$\Large \frac{d}{dx}C(定数)=0$$
つまり
定数の微分は0
になります。
べき関数の微分
べき関数とは
$x^{n}$のような形の関数です。
$$\Large \frac{d}{dx}x^{n} = nx^{n-1}$$
サインの微分
$$\Large \frac{d}{dx}\sin x = \cos x $$
コサイン微分
$$\Large \frac{d}{dx}\cos x = -\sin x$$
指数関数の微分
$$\Large \frac{d}{dx}e^{x} = e^{x} $$
この$e$は
自然対数
と呼ばれる定数です。
上式のように
その指数関数は
微分しても
形が変わらない
という著しい特徴を持ちます。
その他大事な微分
関数の和の微分
$$\Large \frac{d}{dx}\{f(x)+g(x)\}= f'(x)+g'(x)$$
つまり2つの関数の和
を微分する際は
それぞれを
個別に微分して足す
関数の積の微分
$$\Large \frac{d}{dx}f(x)g(x) =f'(x)g(x)+f(x)g'(x) $$
つまり2つの関数の積
となっている場合には
片方ずつ微分して足す
ということになります。
関数の中にさらに関数を含む場合
$$\Large \frac{d}{dx}f(z)= \frac{dz}{dx}\frac{df}{dz} $$
$$ {(zはxの関数)}$$
これに関しては具体例をあげた方が
わかりやすいと思うので
以下にその具体例を挙げます。
$例)(3x^{2}+6)^{5}の微分$
\begin{equation}
\begin{split}
\large \frac{d}{dx}(3x^{2}+6)^{5} &= (3x^{2}+6)’ \times 5(3x^{2}+6)^4 \\
\large &= 6x \times 5(3x^{2}+6)^4
\end{split}
\end{equation}
というようになる。
これはつまり$(3x^{2}+6)^{5}$の微分は
$(3x^{2}+6)$をひとかたまりに見て
$z=(3x^{2}+6)$と置くと、
中身($z$)の微分
を実行し、それに
外側($z^{5}$)の微分
をかけることで
求まるわけです。
微分の解説は以上になります。



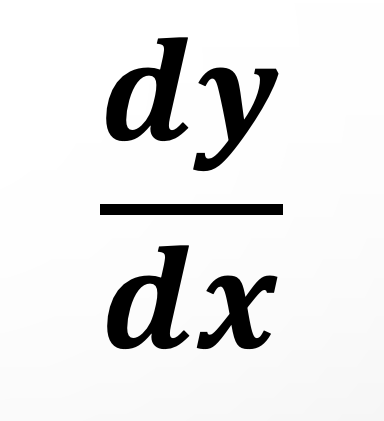












コメントを残す