質量が0だと紐や糸の張力が両端で等しくなる理由＆至る所で張力が等しくなる理由

ひもの張力はどこでも同じになる

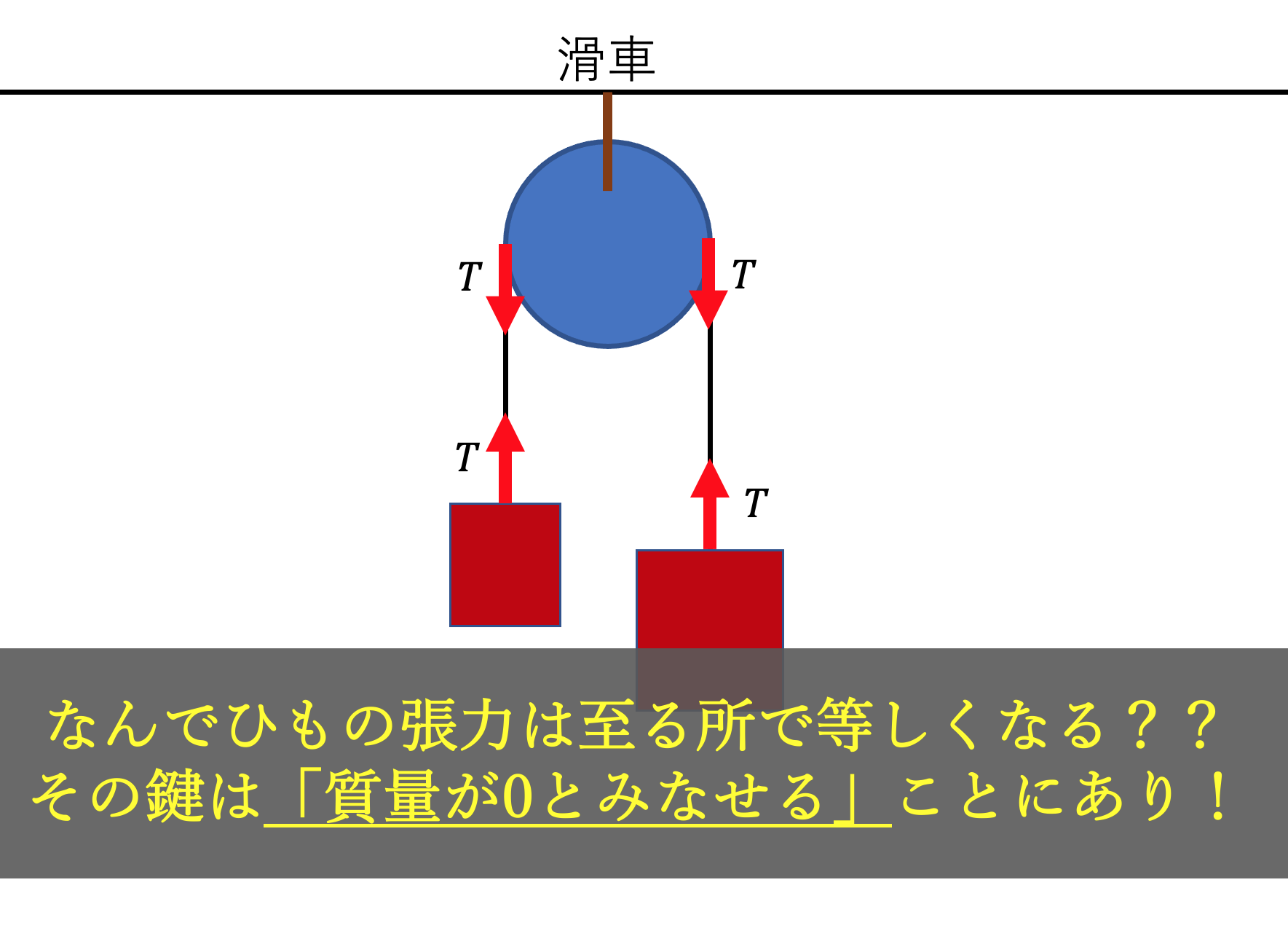
ひもが滑車を通して2つの物体を支えている
次のような状況を考えましょう。

結論からいうと高校物理においては
この時2つの物体に働く張力$T$は
まったく同じになります。

さらに張力というのは
次のように

ひものいかなる場所においても
同じ大きさ

になります。

今回は、このように

ひもの張力が
どこでも同じになるわけ

や

ひもの両端の張力が
等しくなるわけ

についてわかりやすく解説していきます！

「ひもの質量は無視できる」の意味

この

ひもの張力は
どこでも一緒になる

というのは実は
普段問題文中に何気なく書いてある

「ひもの質量は無視できる」

という文言によって保証されています。

それをしめすために次のような
質量 $m$、長さ $l$のひもによって
力 $F$でで引っ張られる質量 $M$の物体を考えます。

また、この時ひもは一様な密度を持っているとします。

それではまず、

ひもと物体を
1つにまとめたもの

の運動方程式を考えましょう。

これに働く力はFであり、
その全質量は$M+m$なので運動方程式は

$$\large (M+m)a=F$$

と書くことができます。

では次にひもの端から
長さ $x$だけ離れた位置での張力を考えていきます。

次の図のように
物体と糸の端から $x(<l)$までを1つにまとめ、
また、その張力をTとします。

するとこの部分の運動方程式は
ひもの質量が$\frac{x}{l}m$と書けることに注意すると

$$\large (M+\frac{x}{l}m)a=T$$

と書くことができます。

ここまでで得られた2つの式を並べてみましょう。

$$\Large (M+m)a=F$$

$$\Large (M+\frac{x}{l}m)a=T$$

ここで、2つの式に現れる加速度$a$は
（同じ物体の加速度なので当たり前ですが）
同じであることに気をつけてください。

これらから加速度 $a$を消すために
2つの式を次のように変形します。

$$\Large a=\frac{F}{M+m}$$

$$\Large a=\frac{T}{M+\frac{x}{l}m}$$

この2つ式をつなげることにより

\begin{align}
\large \frac{T}{M+\frac{x}{l}m}&\large =\frac{F}{M+m}\\
\\
\large T&\large=\frac{Ml+mx}{(M+m)l}F\\
\end{align}

が得られます。

ここで再度述べておきますが
今、上の式は

質量$m$を
持っているひもの張力

を表していることに注意してください。

では

質量をもっていない
ひもの張力

を考えるために、上の式において

$$\Large m=0$$

を代入してみましょう。

すると

\begin{align}
\large T&\large =\frac{Ml+0 \dot x}{(M+0)l}F\\
\\
\large T&\large =\frac{Ml}{Ml}F\\
\\
\large T&\large =F\\
\end{align}

が得られます。

これはxの値にはよりません。

このことから$x$がどんな値でも、
言い換えると

ひものどの位置でも
ひもの質量がない場合には
ひもの張力は同じになる

ということが導かれました。

その結果、物体に働く張力というのは
糸が引っ張られる力$F$に等しくなります。

ひもの両端の張力が等しい理由

では次に、

ひもの両端の
張力が等しいわけ

について解説していきます。

具体例として、簡単のため次のような
糸がたるむことなく繋がれている
2つの物体A、Bを考えてみてください。

（滑車を通して繋がれている
2つの物体を考える場合にも
以下の議論を拡張して
同じことをしめすことができます）

ではこの状況において右向きを正
糸の質量を $m_s$ とし、

糸の運動量方程式

を考えてみます。

物体$A$、$B$に働く張力をそれぞれ
$T_A$、$T_B$と書くことにします。

すると糸に働く力は次のようになります。

糸に対して水平方向に働く力は
$T_A$、$T_B$だけなので
糸の運動方程式は、その加速度を$a$と書くと
（右向きが正であることに注意して）

$$\Large m_s a＝ T_B-T_A$$

となります。

ひもの質量が0の場合

では、先程の得られた運動方程式において

ひもの質量が0の場合

を考えてみます。

これは、運動方程式に
$m_s=0$を代入すればいいので

\begin{align}
\large 0&\large =T_B-T_A\\
\\
\large T_A&\large=T_B\\
\end{align}

を得ることができます。

このように、

糸の質量が0であれば

糸に働く両端の力が等しいわけなので
糸の両端で2つの物体に働く張力は等しくなります。

ひもの質量が0″でない“場合

ひもの質量が0となる場合には
両端の張力が等しくなることがわかりました。

では、ここからより理解を深めるために
逆の場合、すなわち

ひもの質量が0でない場合

ではどうなるかを考えていきます。

先程と同じように運動方程式を考えると

$$\Large m_s a＝ T_B-T_A$$

をえることができます。

ただし、今の場合$m_s\neq 0$であることから
この式は、

両端の張力の大きさは
必ずしも等しくならない

ということを表しています。

このように糸に質量があるかないかで

ひもの両端の張力が
等しくなるかどうか

というのは変わります。

このように糸（ひも）の質量というのは
意外にも重要なので
張力が関わってくる問題を考える際には
このことを意識しましょう。

また、今回は話を簡単にするために

水平方向に
糸で繋がれた2つの物体

を考えましたがが、
同様のことは、次図のような

滑車で繋がれた2つの物体

の場合でも言えます。

ただし、この場合には
糸の運動方程式において

糸に働く重力

を余計に考えないといけません。

もし時間に余裕があれば
こちらも考えてみるとより理解が深まると思います。

まとめ

それでは今回のまとめです。