連結ばね（直列型・並列型・サンドイッチ型）の「ばね定数」の求め方は？問題の解き方は？

合成ばね・連結ばねのバネ定数一覧

合成ばね、または連結ばねのばね定数を
結論から述べると次のようになります。

（ばねの数が2つの場合）

これらは暗記するしかないと
思っている人もいるかもしれませんが
そんな必要はありません。

先程の表のようになる
理屈はとても簡単です。

ばね定数の求め方

それではこれからは
上にあげたばね定数を実際に
求めていきます。

これ以降で一貫した
大切な考え方は

複数のばねを
1つのばねに見なしたい

ということです。

これを念頭に読んでいってください。

直列ばねの場合

では最初は直列ばねについてです。

状況としては次のように
質量$m$の物体を
ばね定数が$k_1$であるばね1と
ばね定数が$k_2$であるばね2が

直列に連結している

状態で支えている場合を考えます。

そして、今これを次のように

1つのばねに見なしたい

わけです。

ではまず
物体に働く力にだけ
注目してみましょう。

物体には次のように
ばね1からの弾性力と重力
が働き、それらがつり合っています。

そして、ばね1の伸びを$x_1$で表すと
フックの法則よりその弾性力は
$k_1x_1$で表されます。

そのため物体に働く力のつり合いから

$$\large k_1x_1=mg\tag{1}$$

が得られます。

これがばね1と物体において
成り立っている式です。

次にばね2も含めて
考えてみましょう。

ばね2は次のように
ばね1と物体からなる部分全体を
その弾性力によって支えています。

ばね2の伸びを$x_2$で表します。

すると次図のように
赤枠で囲まれる部分に
働く力のつり合いから

$$\large k_2x_2=mg\tag{2}$$

が得られます。

なぜなら

バネの質量は
無視していい
（ほど小さい）

からです。

そのため
ばね2が支える質量というのは
物体の質量だけで済みます。

こうして次の2つの式が得られました。

$$\large k_1x_1=mg\tag{1}$$

$$\large k_2x_2=mg\tag{2}$$

ここからさらに
上の2つの式を次のように変形します。

$$x_1=\frac{mg}{k_1}\tag{1’}$$

$$x_2=\frac{mg}{k_2}\tag{2’}$$

この式を覚えておいてください。

では初めに述べたように
2つのばねを1つのばねに
置き換えていきます。

それを行うにあたり
合成したばね定数を

$$\Large k_c $$

とします。

では今、この1つに合成した
ばねの伸びはいくらでしょうか？

それは単純にばね1とばね2の伸びを
足し算してあげればいいので

$$\large x_1+x_2$$

になります。

それゆえこのばねにおいては
フックの法則から
次の式が成り立ちます。

$$\large k_c(x_1+x_2)=mg\tag{3}$$

ここに先ほどの$(1’)(2’)$式を
代入しましょう。

すると

\begin{align}
k_c(x_1+x_2)&=mg\\
\\
k_c\Big(\frac{mg}{k_1}+\frac{mg}{k_2}\Big)&=mg\\
\\
k_c\Big(\frac{1}{k_1}+\frac{1}{k_2}\Big)&=1\\
\\
\frac{1}{k_1}+\frac{1}{k_2}&=\frac{1}{k_c}
\end{align}

と、このように得たかった
直列ばねについての関係式

$$\Large \frac{1}{k_c}=\frac{1}{k_1}+\frac{1}{k_2}\tag{4}$$

が得られました。

また、先程の(4)式を変形することで

$$\large k_c=\frac{k_1k_2}{k_1+k_2}$$

 も得られます。

直列ばねを横向きにおいた場合はどうなるのか？？

先程までは次のような
直列ばねを考えてきました。

そのため次のような

バネを横に置いた場合

にも成り立つのかと不安に
思う人もいるかもしれません。

もちろんこの場合でも
同様に成り立ちます。

それを証明するためには
次のように力$F$で引っ張られている
状況を考えるといいです。

すると上と同様に、
各ばねが

何を引っ張っているのか

をちゃんと意識し
力のつり合いを考えることで

$$x_1=\frac{F}{k_1}$$

$$x_2=\frac{F}{k_2}$$

が得られ、最終的に

 $$\Large \frac{1}{k_c}=\frac{1}{k_1}+\frac{1}{k_2}$$

という同じ式を得ることができます。

不安な人は実際に
自分で手を動かして
考えてみてください。

並列ばねの場合

並列ばねでは
状況として次のような
ばね定数が$k_1$であるばね1と
ばね定数が$k_2$であるばね2が

並列に
物体とつながっている

場合を考えます。

そして今、次のようにこれを

1つのばねに見なしたい

わけです。

今、ばね1もばね2も
並列につながっているため
ばねは同じだけ伸びています。

そしてその伸びを$x$としましょう。

するとばね1による力は
フックの法則から

$$\large k_1x$$

また、ばね2による力は

$$\large k_2x$$

と表されます。

そして今、直列の場合と違って
2つのバネは
直接物体に力を及ぼします。

それゆえ物体に働く力$F$は
この2つを単純に足し合わせたものになります。

$$\large F=k_1x+k_2x=(k_1+k_2)x$$

それゆえ、今
物体に働く力のつり合いから

$$\large (k_1+k_2)x=mg\tag{5}$$

が成り立ちます。

この(5)式は覚えておいてください。

では次に、

1つのばねだと
見なした場合

について考えます。

直列の場合と同様に
このばねのばね定数を

$$\Large k_c$$

としましょう。

そして今
このばねの伸びは
2つのばねと同じく$x$です。

そのため物体に働く力のつり合いから

$$\large k_cx=mg\tag{6}$$

が得られます。

そして(5)式と(6)式を
比べることにより、容易に

$$\Large k_c=k_1+k_2$$

となり、得たかった
並列ばねの関係式が得られました。

サンドイッチばねの場合

サンドイッチ型のばねの場合は
状況として次のような
ばね定数が$k_1$であるばね1と
ばね定数が$k_2$であるばね2が

物体の両端に
つながっている

場合を考えます。

そして今、これを次のように

1つのばねに見なしたい

わけです。

それでは考えていきましょう。

まず2つのばねの長さは
自然長にあると考えます。

そしてこの状況から

物体に右向きの力$F$を加え
$x$だけ右に物体をずらす

ことにしましょう。

するとばね1では

より伸びようとする
力$k_1x$

が左向きに働き

ばね2では

より縮もうとする
力$k_2x$

が左向きに働ことになり
全体として

$$\large k_1x+k_2x=(k_1+k_2)x$$

の力が左向きに働きます。

そのため力のつり合いから

$$\large F=(k_1+k_2)x\tag{7}$$

が成り立ちます。

この(7)式を覚えていてください。

では次に、

1つのばねだと
見なした場合

を考えます。

これまでの場合と同様に
このばねのばね定数を

$$\large k_c$$

としましょう。

そして今、力$F$を加えて
$x$だけ右に物体をずらすので
力のつり合いから

$$\large F=k_cx\tag{8}$$

が得られます。

この(7)式と(8)式を比べると
容易に

$$k_c=k_1+k_2$$

となり、得たかった
サンドイッチ型のばねの
関係式が得られました。

実際に例題を解いてみる

ここまでで
次の関係式がなぜなりたつか
はわかってもらえたでしょう。

ここからはこの関係式を用いて
実際に例題を解いてみましょう。

問題を解いていく過程では
いきなり3つ以上のばねを
1つのばねだとみなすのではなく

2つのばねを
1つのばねだとみなす

ということに注意してください。

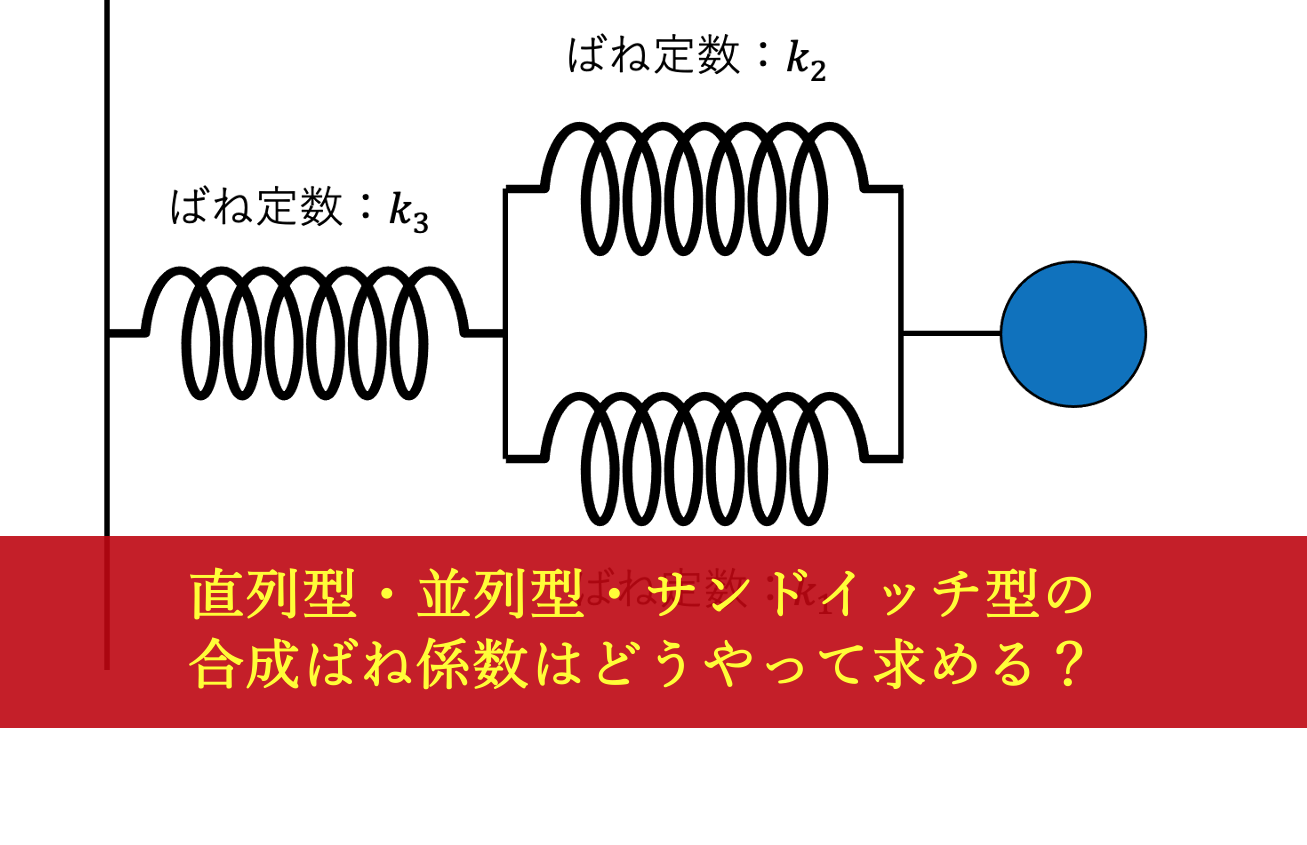
問題

次の合成ばねのばね定数をもとめよ。

解説

この問題には3つのばねがありますが
最初に述べたように

3つのばねを1つにみなす

ということはしないでください。

考えるべきは

2つのばねを1つにみなす

ことです。

それではまず次の部分に注目します。

これは

2つのばねが
並列につながれている

と考えることができます。

それゆえ次の関係式

$$\large k_c=k_1+k_2$$

を用いて、この2つのばねを
1つのばねと見なした場合の
ばね定数を$k’$とすると

$$\large k’=k_1+k_2$$

となり、次の図のようにできます。

これでばねが1つ減り

2つのばねが
直列につながっている

とみなせるようになりました。

直列につながっているので
次の関係式

$$\Large \frac{1}{k_c}=\frac{1}{k_1}+\frac{1}{k_2}$$

が使えます。

最終的に求めたいばね係数を$k$とし
先程の関係式を使うと

$$\large \frac{1}{k}= \frac{1}{k_3}+\frac{1}{k’}$$

変形して

$$\large k=\frac{k’k_3}{k’+k_3}$$

が成り立つので、
先ほど求めた$k’$を代入し
変形して、最終的に$k$は

$$\large k = \frac{(k_1+k_2)k_3}{k_1+k_2+k_3}$$

が得られます。
これが答えになります。

繰り返しますが、
ちゃんと答えに
たどり着くためのポイントは

2つのばねを
1つにみなす

ことを徹底し、絶対に

3つ以上のばねを
いきなり1つにしない

ことです。

冷静に2つ→1つと考えていけば
簡単に解けます。

まとめ

それでは今回のまとめです。