Contents
ばねの単振動の運動方程式
今回は次の図のような
ばねによる単振動
において、運動方程式が
$$\Large ma=-kx$$
と書かれるのはなぜなのかを
丁寧に解説していきます!



フックの法則に
マイナスが
つくってこと?
と混乱している人は必見です!
フックの法則にはマイナスがつく?つかない?
ではまず
「フックの法則とは何か?」
から復習しましょう。
フックの法則とは次のようなものです。
$$\large F=kx $$
$x$:自然長からのばねの伸び
$k$:ばね定数、$F$:弾性力
教科書やwebページによっては
このフックの法則の書き方がやや違うようですが
少なくともこの記事において「フックの法則」
と言う時は、先程の法則を指します。
ここで意識しなければならないのは
フックの法則は
「向き」を考慮してない
ということです。
先程のフックの法則とは
ばねをより伸ばすor縮めれば
より大きな力が生まれる
ことを言っているだけです。
どの向きに
力が大きくなるのか
は教えてくれません。
しかし運動方程式を考えるには
「向き」を考える必要があります。
この点をちゃんと意識せずに
混乱する人が一定数いるようなので
気をつけましょう。
ということでここからは
弾性力の向き
まで考慮して運動方程式を丁寧に作っていきます。
運動方程式を丁寧に作ってみる
わざわざ説明する必要はないとは思いますが
運動方程式とは
$$\large ma=F$$
と書かれるのでした。
そして今$F$は弾性力を表すことになるはずです。
この$F$を考えるために
次のような座標を取りましょう。

今、ばねが自然長となる地点を原点
にとっていることに注意してください。
これから
(ややめんどくさいですが)
ばねが自然長より
伸びている時($x>0$)
と
ばねが自然長より
縮んでいる時($x<0$)
に場合わけをして考えていきます。
$x>0$の時(自然長より伸びている時)
この時、物体に働く力の「大きさ」は
フックの法則より
$$\large |F|=kx~(>0) $$
だとわかります。
(「大きさ」なので絶対値の記号を付けました)
図示すると

のようになります。
そして図からわかるように
この時弾性力は
負の方向
に働きます。
つまり向きまで考慮すると
運動方程式の弾性力には
マイナスをつけないといけません。
ということで物体に働く
向きまで考慮した弾性力
として
$$\large F=-kx$$
が得られます。
$x<0$の時(自然長より縮んでいる時)
では次です。
この場合でも、向きを無視した
物体に働く力の「大きさ」は
フックの法則により
$$\large |F|=-kx~(>0)$$
となります。
今 $x<0$であることから
$kx<0$、また$-kx>0$
であることに注意して下さい。
そしてこれを図示すると
次のようになります。

図からわかるように、この時弾性力は
正の方向
に働きます。
そのため方向を考慮し
運動方程式に用いる際
符号を変える必要はありません。
ということで
向きまで考慮した弾性力
として
$$\large F=-kx$$
が得られます。
2つの場合をまとめる
以上2つの場合をまとめると
ばねの弾性力は
$$\Large F=-kx $$
と表されることがわかります。
よってこれを運動方程式に代入して
$$\Large ma=-kx$$
が得られるわけです。
そしてここから加速度は
$$\Large a=-\frac{k}{m}x$$
となり、さらにこれは$\omega = \sqrt{\frac{k}{m}}$
を用いることにより
$$\Large a=-\omega^2 x$$
が得られます。
ここまで長々と丁寧に解説してきましたが
ばねによって単振動をする物体の
運動運動方程式を考える場合には、とにかく
向きまでちゃんと考慮する
ことに気をつけてください。
まとめ
- フックの法則はあくまで
力の「大きさ」だけ。
その「向き」については
何も教えてくれない。 - 運動方程式では
その「向き」を考慮することで
マイナスが現れる! - その結果、加速度にも
マイナスがつく! - 混乱しないように注意しよう!



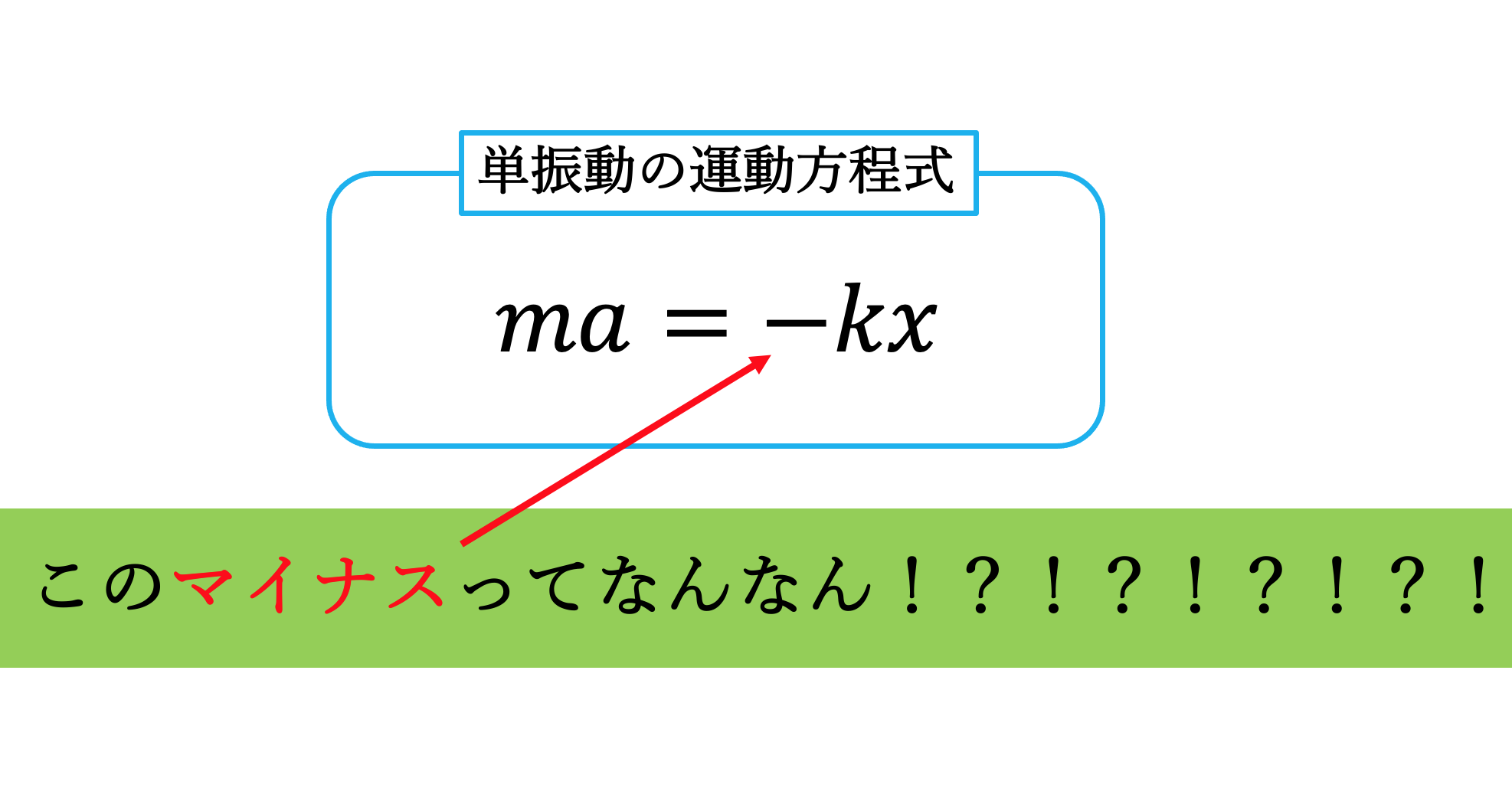













単振動の運動方程式では
なんでばねの弾性力に
マイナスがつくの??