あの「微積物理」を無料で学べます！！
今回は力学における
微積物理の集大成とも言える
単振動
について解説していきます。
Contents
単振動とは
単振動とは次の画像のように
時間と共に変位（位置）が
振動する運動
のことを言います。
よくある単振動の例は
振り子やバネで繋がった物体などです。
単振動には三角関数
先ほどのグラフの
単振動をする物体の変位（位置）の時間変化を
結論から書くと次のような数式で表されます。
$$\Large x \small (t) \Large = A\sin \omega t + B \cos \omega t$$
$$\Large (A, B, \omega は定数)$$
ひとまず、これらに登場する
定数の意味は置いておきます。
上式を見て
と混乱している人もいるかもしれませんが
これは
三角関数の合成
を思い出すとよくわかります。
先ほどに式において
三角関数の合成を行うと
\begin{equation}
\begin{split}
&\Large A\sin \omega t + B \cos \omega t \\
\\
&\Large = C \sin ( \omega t+ \alpha )\\
\end{split}
\end{equation}
$$\large ここで、C=\sqrt{A^{2}+B^{2}}$$
というように、1つの三角関数で
表すことができます。
この$\alpha$は以下の画像のように
初期の位置を表す適当な定数です。
このように描かれれば
三角関数のグラフを一度でもみたことのある場合
単振動の時間変化が三角関数で表されることに
なんとなく納得がいくと思います。
しかしまだ「なんとなく」です。
これからそれをもっとクリアにしていきます。
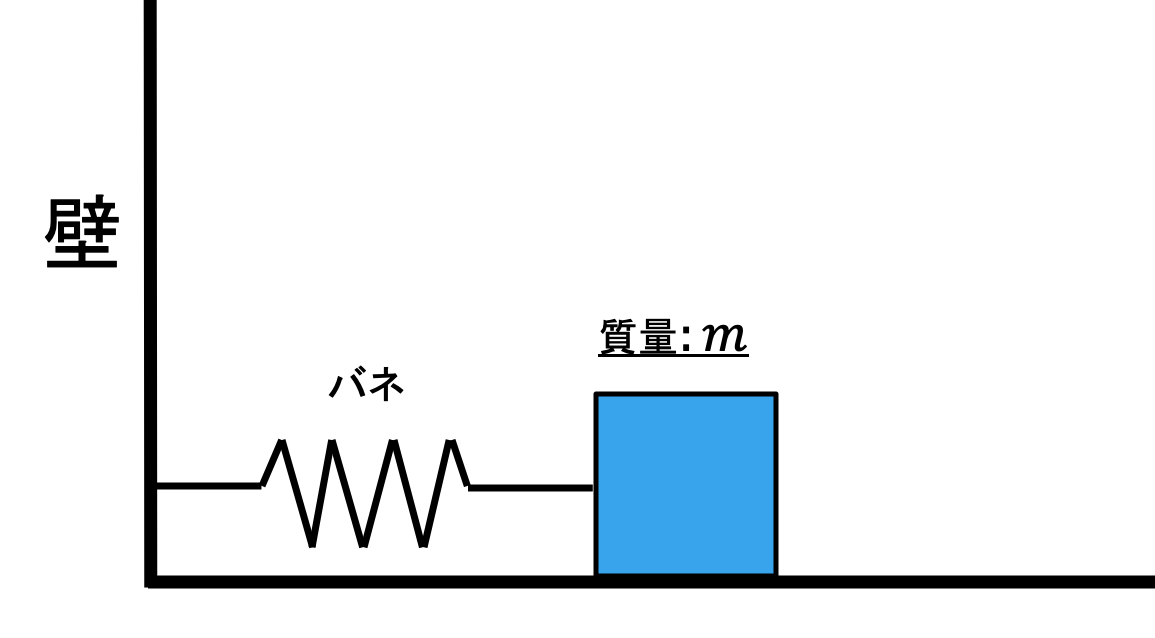
壁にバネで繋がった物体
まず次のような物体を考えます。
最初バネは自然長にあったとして
その長さを$\large x_0$とします。
そしてそこから少しずらし物体を運動させます。
ただし地面との摩擦はありません。
このような状況において物体の運動を考えてみましょう。
まず物体に働く力を書いてみましょう。
この時物体に働く力は
重力
垂直抗力
バネの弾性力
この3つです。
図示すると次のようになります。
では次に、自分で座標をとって
正の向きを決めます。
この場合次のような座標をとることにします。
ではこの場合の運動方程式
を立てていきましょう。
１つ注意なのが、今回の場合
$x$方向だけではなく$y$方向も考える必要があり、
そのため運動方程式は２つになる、ということです。
$x$方向に1つ、$y$方向に1つ運動方程式を
立てなくてはなりません。
この場合大事なのは$x$方向の運動なので
まずはそこから解説し
最初は$y$方向のことは忘れてください。
後でy方向の運動については解説します。
$x$方向の運動
ではまず$x$方向からです。
先ほどの力を書いた画像において
$x$方向のみに注目すると
次のようになります。
このバネのバネ定数を$\large k$
自然長$x_0$からの伸び（または縮み）を$x$
とするとバネの弾性力の大きさは
$$\Large (弾性力の大きさ)= kx$$
と表されます。
ただこの場合先ほど図示したように
弾性力は負の方向を向いているので
物体に働く力は
$$\Large F= -kx$$
です。
これを運動方程式に代入すると
$$\Large m\ddot{X}= -kx$$
$$\large (X=x_{0}+x)$$
となります。
ここでなぜ$x$ではなくて
$X$なのか疑問に思ったでしょう。
その理由は
$x$は物体の位置を
表していない
からです。
$x$の意味を思い出すと次の画像のように
自然長$x_0$からの
伸び、または縮み
を表すのでした。
つまり自然長のところで$x$は0になります。
そしてそれより右では正に
左では負になります。
しかしこの場合
位置の原点$(X=0)$は壁になるように
座標をとったはずです。
このように$x$は
物体の位置とは別物
ということに注意してください。
そして物体の位置とは
バネの自然長$(x_0)$にバネの伸び$(x)$
または縮みを加えたものです。
つまり次のように表されます。
$$\Large X= x_0 + x $$
$$\large (縮んでいる時はx＜０)$$
そして運動方程式は以下のようになります。
$$\Large m \frac{d^{2}}{dt^{2}}(x_0 + x) = -kx$$
ここで右辺の次の微分に注目しましょう。
$$\Large \frac{d^{2}}{dt^{2}}(x_0 + x) $$
これを計算していきます。
すると
$$\Large \frac{d^{2}}{dt^{2}}(x_0 + x) = \frac{d^{2}}{dt^{2}}x_0 + \frac{d^{2}}{dt^{2}}x\small (t)$$
$x_0$は定数なので
定数の微分として０となり消えます。
よって
\begin{equation}
\begin{split}
\Large \frac{d^{2}}{dt^{2}}(x_0 + x) &= \Large \frac{d^{2}}{dt^{2}}x\small (t)\\
\\
\Large &= \Large \ddot{x}
\end{split}
\end{equation}
このことからさらに運動方程式を書き直すと
$$\Large m\ddot{x}= -kx$$
となります。
さぁこれで運動方程式の完成です。
運動方程式さえ立てることができれば
あとはもう悩む必要はありません。
計算を行うだけです。
運動方程式を解く
先ほど立てた運動方程式を詳しくみてみましょう。
$$\Large m\ddot{x}= -kx $$
両辺を$\large m$で割り、次のようにします。
$$\Large \ddot{x}= -\omega^{2}x$$
$$\large \omega ＝\sqrt{\frac{k}{m}}$$
$\omega$の意味については後ほど解説。
これは$\large x \small (t)$を求める微分方程式ですが
実は今までのように
両辺を積分するやり方ではうまくいきません。
この場合ちょっとした推測
が必要になります。
先ほどの運動方程式を眺めると
$x$を二回微分すると
元の関数$x$に戻って定数$\omega$がつく
ことが読み取れますよね？
このことから
二回微分すると
元に戻りそうな関数
を考えてみます。
この時思い出して欲しいのが
三角関数の微分
です。
三角関数の微分は次のようになるのでした。
$$\Large \frac{d}{dt}\sin t = \cos t $$
$$\Large \frac{d}{dt}\cos t = -\sin t$$
つまり三角関数は微分するごとに
（符号は別として）
サイン→コサイン→サイン→コサイン→…
というように交互に入れ替わると言えます。
つまりサインを2回微分すると
サインに戻りますし、
コサインを2回微分すると
コサインに戻ります。
この性質は先ほどの運動方程式において
みられる性質と同じです！
ということでサインとコサインを両方含む
以下の式を運動方程式の
左辺に試しに代入してみましょう。
$$\Large x \small (t) \Large = A\sin \omega t + B \cos \omega t$$
$$(A,Bは定数)$$
すると
\begin{equation}
\begin{split}
\Large \ddot{x}&\Large = \frac{d^2}{dt^{2}}(A\sin \omega t + B \cos \omega t) \\
\\
&\Large = \frac{d}{dt}(A\omega \cos \omega t – B\omega \sin \omega t)\\
\\
&\Large = -A\omega^{2} \sin \omega t – B\omega^{2} \cos \omega t\\
\\
&\Large = -\omega^{2}(A\sin \omega t + B \cos \omega t) \\
\\
&\Large = -\omega^{2} x
\end{split}
\end{equation}
となり確かにこれは運動方程式の
解であることがわかります。
ついでに三角関数の合成をした
次の式
$$\Large x \small (t) \Large = C\sin(\omega t + \alpha ) $$
も同じように代入してみましょう。
すると
\begin{equation}
\begin{split}
\Large \ddot{x}&\Large = \frac{d^{2}}{dt^{2}}C\sin(\omega t + \alpha )\\
\\
&\Large = \frac{d}{dt}\omega C\cos(\omega t + \alpha )\\
\\
&\Large = -\omega^{2} C\sin (\omega t + \alpha )\\
\\
&\Large = -\omega^{2}x
\end{split}
\end{equation}
となりこれも運動方程式の解だとわかります。
このようにして単振動の運動方程式は
解かれ、その運動を表す数式
$$\Large x \small (t) \Large = A\sin \omega t + B \cos \omega t$$
$$(A,B は定数)$$
または
$$\Large x \small (t)= \Large C\sin(\omega t + \alpha ) $$
$$(C, \alpha は定数)$$
が得られます。
ここで$\omega$は角振動数と言い、
これは振動の速さを表しており
角振動数が大きければその振動は速く
角振動数が小さければその振動は遅いことを意味します。
速度の式を導く
速度は
変位を
時間で微分したもの
でした。
つまり
$$\Large x \small (t) \Large = A\sin \omega t + B \cos \omega t $$
の両辺を時間で微分すると速度になります。
ということで
両辺を時間で微分すると
$$\Large \dot{x} = \omega A\cos \omega t – \omega B \sin \omega t$$
$$（合成関数の微分）$$
となり、これが速度になります。
$$\Large v \small (t) \Large = \omega A \cos \omega t – \omega B \sin \omega t$$
加速度の式を導く
運動方程式から明らかではありますが
念のため、別のアプローチで
単振動の加速度を求めていきます。
加速度は
速度を時間で微分すると
得ることができます。
そこで先ほど求めた
$$\Large v \small (t) \Large = \omega A \cos \omega t – \omega B \sin \omega t$$
の両辺を時間で微分します。
すると
\begin{equation}
\begin{split}
\Large \dot{v} & \Large = \ddot{x} \\
\\
&\Large = -\omega^{2}A \sin \omega t – \omega^{2} B \cos \omega t \\
\\
&\Large = -\omega^{2}(A \sin \omega t + B \cos \omega t)\\
\\
&\Large = -\omega^{2}x
\end{split}
\end{equation}
となりこれが加速度の式となります。
$$\Large a=-\omega^{2}x$$
定数を求める
次に定数$\large A,B$を求めていきましょう。
ここで運動方程式を解くために
必要な事項を思い出してください。
そう。その条件とは
初期条件
のことです。
このことがピンとこない方は
こちら
先ほどの求めた式は以下のようなものでした。
$$\Large x \small (t) \Large = A\sin \omega t + B \cos \omega t$$
$$(A,Bは定数)$$
ここで初期$(t=0)$の変位(位置)を考えてみましょう。
先ほどの式に$t=0$を代入して
$$\Large x \small (0) \Large = B $$
よって
$$\Large B = x \small (0)$$
であることがわかり$\large B$は
初期位置を表すことがわかりました。
次に$\large A$についてです。
先ほどは初期の変位を考えましたが
今回は初期の速度（初速度）
を考えていきます。
速度は次式で与えられるのでした。
\begin{equation}
\begin{split}
\Large v \small (t) &\Large = \dot{x} \\
\\
&\Large =\omega A \cos \omega t – \omega B \sin \omega t $$
\end{split}
\end{equation}
ここに$t=0$代入します。
すると
$$\Large v\small(0) \Large = \omega A$$
よって$\large A$の値は
$$\Large A= \frac{v\small(0)}{\omega}$$
と求まります。
以上の値を元の式に代入すると
最終的ににもとまる式は次の式になります。
$$\Large x\small (t) \Large = \frac{v\small(0)}{\omega} \sin \omega t + x \small (0) \Large \cos \omega t $$
仮に最初自然長から$L$だけ伸ばし、
初速度０で運動をさせた、つまり
$\large x \small (0) \large = L , v \small(0) \large = 0$
という場合には
$$\Large x\small (t) \Large = L \cos \omega t $$
となり、見慣れた形になります。
変位には要注意！
先ほど求めた次の式
$$\Large x\small (t) \Large = \frac{v\small(0)}{\omega} \sin \omega t + x \small (0) \Large \cos \omega t $$
で満足したくなるかもしれません。
だがしかし！
このままでは終われません。
というのも既に述べましたが
$x$は物体の位置ではなく、
バネの自然長からのズレ
を表しているからです。
そのため先ほど設定した座標において
物体の位置$X$を求めるのなら、
$$\Large X= x_0 + x \small(t) $$
より
$$\Large X \small(t) \Large = x_0 + \frac{v\small(0)}{\omega} \sin \omega t + x \small (0) \Large \cos \omega t $$
となります。
自分が最終的に得たいものはなんなのか
その変数が意味するものはなんなのか、
ということに注意しましょう。
座標を変えれば答え方ももちろん変わる
先ほどは次の画像のように
壁を原点としたために
$$\Large X \small(t) \Large = x_0 + \frac{v\small(0)}{\omega} \sin \omega t + x \small (0) \Large \cos \omega t $$
というように変位は表されました。
しかしこの表記はぶっちゃけ
$\large x_0$が邪魔です。
そこで先ほどとは違って次のように
座標を取り直して考えてみましょう。
この時自然長の位置が原点です。
つまり縮んでいる時、物体の位置は負であり
伸びている時、物体の位置は正です。
このようにすると
バネの自然長からのズレ
＝物体の位置
つまり
$$\Large X = x\small (t) $$
となるので運動方程式は
$$\Large m\ddot{x}= -kx$$
となり、これまでと同じように
運動方程式を解いて
$$\Large x\small (t) \Large = \frac{v\small(0)}{\omega} \sin \omega t + x \small (0) \Large \cos \omega t $$
となり今回は
これだけで物体の位置を表します。
このように
座標の取り方次第で
表現の仕方が変わることに注意してください。
ただし
実際に起こっていることは
同じである
ことには注意です。
あくまで変わるのは
表し方だけです。
$y$方向の運動
それでは蔑ろにしていた$y$方向について
丁寧に解説していきます。
$y$方向に働く力は
重力と垂直抗力です。
鉛直上向きが正であることに
注意すると$y$方向の力は
$$\Large F = N – mg$$
と書けます。
これを基に運度方程式を立てると
$$\Large m\ddot{y}= N – mg $$
となります。
(この時$N$の具体的大きさはまだ不明です）
ここで垂直抗力があるので
束縛条件
を考えなくてはいけません。
この場合の束縛条件とは
$y$方向には動かない
というものです。
つまり
$$\Large \ddot{y}=0 $$
が言えます。
これを運動方程式に代入して
\begin{equation}
\begin{split}
\Large 0 = N – mg \\
\\
\Large N= mg
\end{split}
\end{equation}
このようにして$y$方向の力は
つり合っていることがわかり
$y$方向の運動は記述されます。
以上のように、公式を覚える以外に習わないような
単振動も、微積物理では
全て運動方程式によってつながるわけです。
それによって
変位、速度、加速度というように
わざわざ分けて覚える必要も皆無になります。
あの「微積物理」を無料で学べます！！
皆さんの「ここを教えてほしい」を募集しています！
高校物理に関して
「こんなことを教えて欲しい」
「この問題をわかりやすく解説して欲しい！」
「勉強のコツを知りたい！」
などなど、質問を募集しています！
気軽に質問してください！無料です！
質問内容に関しては記事として回答させていただきます！
⚠️質問の回答は先着順で回答していくため、質問から回答までの期間が長くなることがあります。あらかじめご了承ください。
え、なんで
波を表現するのに
サインとコサインを足すの？？