あの「微積物理」を無料で学べます！！
Contents
積分の概説
今回は初学者でもわかるように
積分
について解説していきます。
積分についても微分と同様に
難しい印象を持っているかもしれません。
しかしそんなことないので
難しく考え過ぎないように
読んでいってください。
積分も実はとてもシンプルです。
では、まず次のように
適当な関数（なんても良い）を考えます。
次に、ある区間
$a \leq x \leq b$を設定します。
（これもどこでも良い）
そして次の画像のようにこれらで囲まれた部分の
面積$\large S$を求めていきます。
まず区間を同じ幅で2個に分割して
それによってできる
長方形の集合
を考えてみましょう。
長方形の幅を$\Delta x$とすると
以下の画像のようになります。
ではさらに区間を同じ幅で
4個に分割した場合を考えます。
すると
このようにどんどん分割していき
N個に分割した場合を考えます。
すると
このようになります。
もう気づいた方もいるでしょうが
このようにして長方形を作ると
長方形の面積の合計
が
求めたい面積に近い
ことがわかります。
しかしこれは
近いだけです。
イコールではありません。
これをイコールで結ぶためには
Nを無限に大きくする
つまり
無限個に分割して
無限個の長方形の
合計を考える
ようにするとイコールで結ぶことができます。
この時分割の幅$\Delta x$は
無限個に分割するわけなので
必然的に無限に小さくなります。
つまりこの状況は
次の画像のように
もはや直線と
みなせる長方形が
無限個並んでいる状態
と言えます。
では、これらを数式で
書くとどうなるでしょうか。
N個の長方形で分割する場合は
左からn番目の長方形の位置を$\large x_n$
で表すと、その長方形1つの面積は
$$\Large (縦\times 横)=f(x_n)\Delta x$$
と表されるので、
それら全てを足し合わせた全体の面積は
和を表すΣ（シグマ）（下の補足参照）
の記号を用いて
$$\Large 面積の和= \sum_{n=0}^N f(x_n) \Delta x $$
$$(x_0=a, x_N=b)$$
と書き表されます。
このΣは$f(x_n)$を
$x_n$の多項式とすると
$$\Large \sum_{n=0}^N f(x_n) $$
で
$f(x_n)$を$n$について
$n=0$から$N$まで足し合わせる
つまり、
$$ \sum_{n=0}^N f(x_n) =f(x_0)+f(x_1)+\cdots + f(x_n)$$
ということを意味します。
そして先程の
分割の数を
無限個に増やす操作
は
$$\Large \lim_{N \to \infty, \Delta x \to 0 } \sum_{n=0}^N f(x_n) \Delta x $$
というように表されます。
そしてこれこそが
積分の操作
に相当します。
つまり積分とは
インテグラル（ $\int$ ）という記号を用いて
$$ \int_a^b f(x) dx = \lim_{N \to \infty, \Delta x \to 0} \sum_{n=0}^N f(x_n) \Delta x$$
$$(ただしx_N=b,~~x_0=a)$$
のように表されます。
このインテグラルの記号の意味は
無限小を無限個
足し合わせる
ことだと考えると良いです。
$dx$は
微分でも説明したように
微小(無限に小さい)な$x$
を表し、$f(x)$は関数の値であるので
$\Large f(x)dx$
は次のように
横が$dx$
縦が$f(x)$である
無限に細い長方形の面積
であると言えます。
（無限に細いわけなのでもはや一本の線）
そして先に述べたように
この無限に細い長方形を
無限に並べる
ことで求めたい面積を作れることができ
$$\int$$
がこれらを全て足し合わせることを意味します。
これが積分であり、この場合
『$f(x)$をaからbまで積分する』
と言います。
ここで一つ注意しなければなりません。
考えやすさのため
積分とは面積だ
という風に述べてきました。
しかし実際には次のような関係にあります。
つまり面積は積分の
要素の一部でしかありません。
例えば負の範囲にある関数では
縦に当たる部分が負になるので
負の面積というあり得ないことになります。
本当の積分とは
無限に小さい$f(x)dx$
を
$\int$で無限に足し合わせる操作
のことです。
無限に小いものを
無限に足し合わせるので
有限の数字
を求めることができます。
ここでよく$dx$を書き忘れがちです。
しかし$dx$をかけないと
無限に小さい量
にはならないので忘れないように。
以上が積分の説明になります。
ここまででわからない箇所があれば
遠慮せず質問してください！
具体的な積分の公式
以下に物理でよく使う積分の公式を載せます。
物理ではただの計算と
してでてくるので、以下の公式は
なんかよくわからんけど
成り立つもの
ぐらいの感じで割り切って
覚えちゃいましょう。
数学の勉強を進めていけばいずれ
以下の公式の証明も勉強することになります。
以降に積分定数Cが出てきますが
それについては次の記事で解説しています。
リンク
とりあえずは、
「そういう形になるんだな」
と納得しておいてください。
定数
$$\Large \int Adx = Ax + C {(Aは定数)}$$
べき関数
$$\Large \int x^n dx = \frac{1}{n+1}x^{n+1} +C $$
サイン
$$\Large \int \sin x dx = -\cos x + C $$
コサイン
$$\Large \int \cos x dx = \sin x + C $$
指数関数
$$\Large \int e^x dx = e^x +C$$
変数が定数倍された関数
$$\Large \int f(ax) dx = \frac{1}{a}F(ax) + C$$
$$\Large \int f(x)dx = F(x) + C $$
このような関係にある$F(x)$を
$f(x)$の原始関数
と言います。
2種の積分（定積分と不定積分）
積分には2種類あります。
それが
定積分
と
不定積分
です。
まず定積分とは次のように
積分する範囲が
決まっている積分
です。
\begin{equation}
\begin{split}
\Large \int_a^b f(x)dx &= \Large \left[ F(x) \right]^b_a \\
&\Large = F(b)-F(a)
\end{split}
\end{equation}
次に不定積分とは次のような
積分する範囲が
決まっていない積分
です。
$$\Large \int f(x)dx = F(x) + C $$
見比べると明らかなように
定積分では定数はつかず
ただ1つの「値」を知ることができる
のに対して
不定積分では定数がつき
1つの「関数」を知ることができる
という違いがあります。
物理において、わかると便利なのは「値」よりも「関数」であるので、
関数を求めることができる不定積分がより重要です。
あの「微積物理」を無料で学べます！！
皆さんの「ここを教えてほしい」を募集しています！
高校物理に関して
「こんなことを教えて欲しい」
「この問題をわかりやすく解説して欲しい！」
「勉強のコツを知りたい！」
などなど、質問を募集しています！
気軽に質問してください！無料です！
質問内容に関しては記事として回答させていただきます！
⚠️質問の回答は先着順で回答していくため、質問から回答までの期間が長くなることがあります。あらかじめご了承ください。
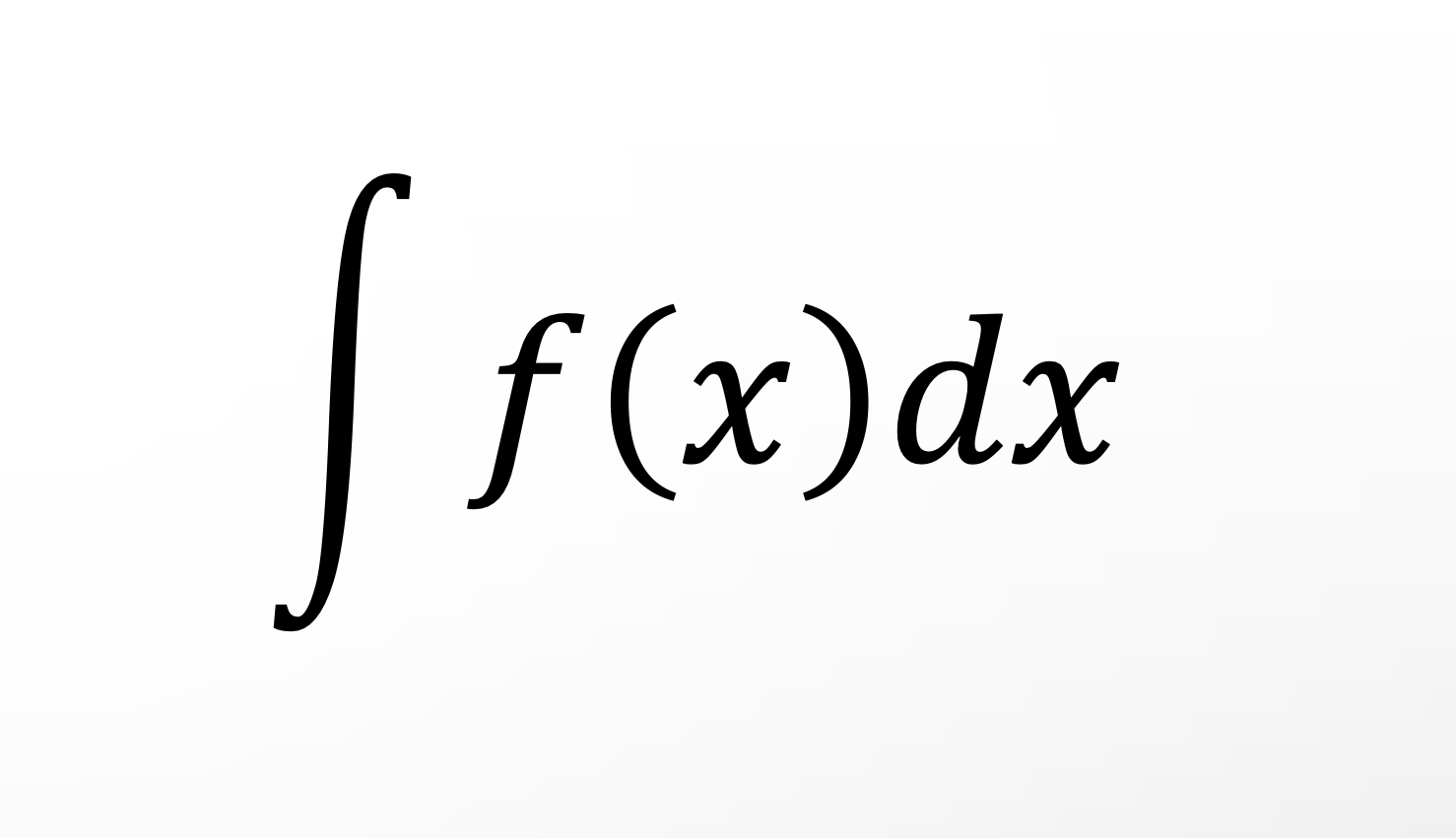
コメントを残す