あの「微積物理」を無料で学べます！！
今回は物理全体において重要な
間違わない力の書き方
について解説していきます。
多くの人が
間違った力の書き方
をしてしまっているために
混乱して余計な失点をしているので
気をつけてください。
Contents
力の書き方３ステップ
力を図に書き込んでいく際には
次の3つのステップを踏むようにしましょう。
ステップ①
注目する物体を1つ決める
ステップ②
重力を書く
ステップ③
存在するなら抗力・張力・摩擦力を書く
以下このそれぞれについて
詳しく解説していきます。
注目する物体を1つ決める
ここでいう
注目する物体
というのは力を書き込もうと
している物体のことです。
例えば次のような物体を考えてください。
この物体に力を書き込んでいく際
まず
Aに働く力を考えるのか
Bに働く力を考えるのか
Cに働く力を考えるのか
これらをちゃんと決める必要があります。
そして、例えば
Bに働く力を考える
と決めたなら、
AとCに働く力は一旦無視
しなくてはなりません。
つまり
1つ1つの物体に関して
働く力を考慮する必要がある
わけです。
力の書き方を間違える人は大抵の場合
A、B、C全てに働く力を
同時に考えている
ことが原因となっています。
同時に考えた結果、混乱を招き
不要なところで失点をしている状態です。
なので、重要なので繰り返しますが
力を考える際は
注目する物体を
まず１つ決めること
そして
注目する物体以外は
一旦無視すること
を心がけましょう。
重力を書く
注目する物体を決めたら
とりあえずまずは
重力を書き込む
ようにしましょう。
この時重力以外の力は
ひとまず無視してください。
重力の書き方としては、次のように
物体の重心から真下に
矢印を書きましょう。
物体が斜めであろうと
重力は真下にしか
働かない
ということに注意してください。
抗力・張力・摩擦力を書く
重力を書いたら最後に
抗力・張力・摩擦力
を考えましょう。
ここでいう抗力とは
全て垂直抗力だと
思ってもらって大丈夫です。
そして張力とは物体が糸で
繋がっている際、糸の方向に生まれる力です。
摩擦力は摩擦のある面上
で発生する力のことです。
以下では特に垂直抗力
について考えていきます。
考えるのは先ほど示した次のような場合です。
この時、手順通りに
注目する物体はBとし
重力を書き込みます。
これで垂直抗力を考える準備ができました。
垂直抗力は
他の物体と
接している面全て
で例外なく発生します。
そしてこの時Bは
AとCに上面と下面で接しています。
上面と下面からの抗力をそれぞれ
$\large N_1,N_2$とすると
この時Bが受ける抗力は
次のようにかけます。
その大きさ自体は
まだ無視して大丈夫です。
力の大きさ自体は
AとCに働く力も考慮することで
求まります。
ともかく以上のようにして
物体に働く力
は間違いなしに書くことができます。
抗力の大きさを求める
では先ほどの例において
垂直抗力の大きさ
も求めていきましょう。
上で説明した手順を元に
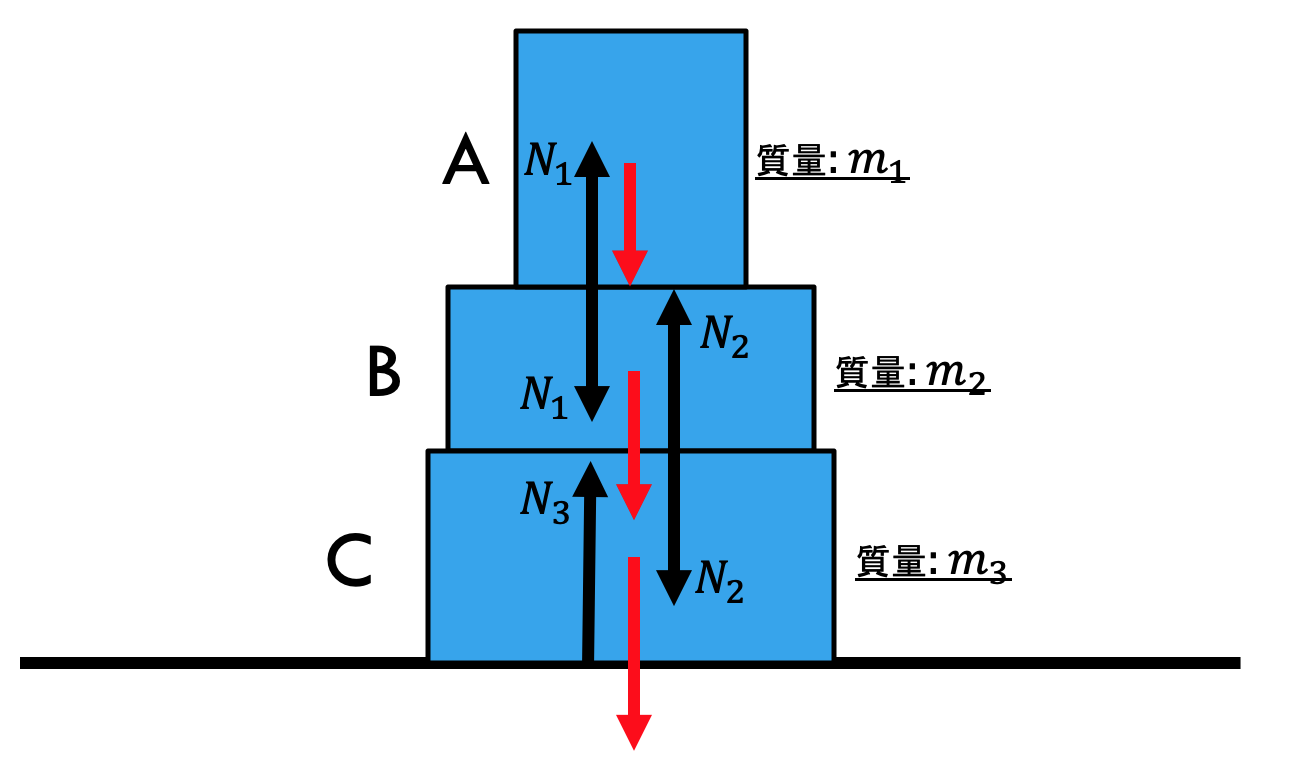
A、B、Cすべてに働く力を記入すると
次のようになります。
(重力の大きさは省略）
ここでAB間、BC間に働く垂直抗力は
等しくなるように書きましたが、これは
作用反作用の法則
に基づいています。
ピンとこない方は要復習です。
作用反作用の法則は軽くみられがちですが
かなり重要な法則でいつでも例外なく成立します。
では本題に戻ります。
まず物体Aについて
つり合いの式
を立ててみましょう。
すると
$$\Large m_1 g= N_1$$
となり、$N_1$の大きさがわかりました。
次にBについて同様に
つり合いの式を立ててみましょう。
すると、左辺には下向きの力
右辺には上向きの力をまとめて
$$\Large m_2 g + N_1 = N_2$$
となり、ここに先ほどの$N_1$を代入して
$$\Large N_2 = m_1 g+ m_2 g$$
という風に$N_2$の大きさが求まります。
最後にCについて同様に
つり合いの式を立てると、
左辺に下向きの力
右辺に上向きの力をまとめて
$$\Large m_3 g + N_2 = N_3 $$
となり、ここに先ほどの
$N_2$を代入すると
$$\Large N_3 = m_1 g+ m_2 g + m_3 g$$
という風に$N_3$の大きさがわかります。
この最後の$N_3$の大きさは
ちゃんと3つの物体の重力の和と等しく
直観にも反しないでしょう。
このようにして
力の書き方さえ
間違えなければ
垂直抗力の大きさは
ちゃんと求めることができます。
しかし力の書き方を間違ってしまうと
必ずうまくいかないので気をつけましょう。
間違いやすい・見逃しやすいポイント
最後にこの力の書き方
に関して
間違いやすいポイント
と
見逃しやすいポイント
を紹介します。
なぜ1番上の物体を考慮しないのか
力を書く際に間違いがちな人は
次の図を見て
と疑問を持ちます。
確かに上の図だけ見ると
$\large N_2$によって
「CはBによる力しか受けてない」
と考えたくなるかもしれません。
しかしこれは間違いです。
先ほど示したように$N_2$は
$$\Large N_2 = m_1 g+ m_2 g$$
というように表されます。
ここで$m_1 g$はAに働く重力です。
つまりCに働く$N_2$にはちゃんと
Aからの力（重力）
が考慮されています。
これは次のように
ABを1つにまとめると
わかりやすいでしょう。
すると
力は次のように書けます。
このように書き直すと
Cについて
なんで1番上の物体からの
力は考えないの
という心配は不要であるとわかると思います。
力の書き方で間違いがちな人は
余計な心配を無駄にしてしまう人です。
なのでここで示した手順に沿って
冷静に処理することを心がけてください。
側面にも垂直抗力がある
力を書く際に見落とされがちなものは
側面からの垂直抗力
です。
垂直抗力というのは
接した面に垂直に働く力
をいうのでした。
そのため上で示した次の図では
上面と下面からの垂直抗力を考える必要がありました。
では次のような場合を考えてみましょう。
この図において物体は壁と接しています。
つまり次のように抗力が書けます。
(重力、張力は省略）
このような
側面からの抗力
は見落とされがちです。
しかし
物体が接するところには
必ず抗力が存在する
ので忘れないようにしましょう。
（もちろん接していないのなら抗力は０です）
この抗力の存在を見落としたために
問題が解けない人がいるので
気をつけましょう。
あの「微積物理」を無料で学べます！！
皆さんの「ここを教えてほしい」を募集しています！
高校物理に関して
「こんなことを教えて欲しい」
「この問題をわかりやすく解説して欲しい！」
「勉強のコツを知りたい！」
などなど、質問を募集しています！
気軽に質問してください！無料です！
質問内容に関しては記事として回答させていただきます！
⚠️質問の回答は先着順で回答していくため、質問から回答までの期間が長くなることがあります。あらかじめご了承ください。
CにはAからの力が
働いてるはずなのに
なんで考慮しなくていいの？