Contents
『位置』『速度』『加速度』の関係
今回は物理でお馴染みの
位置
速度
加速度
の関係について解説していきます。
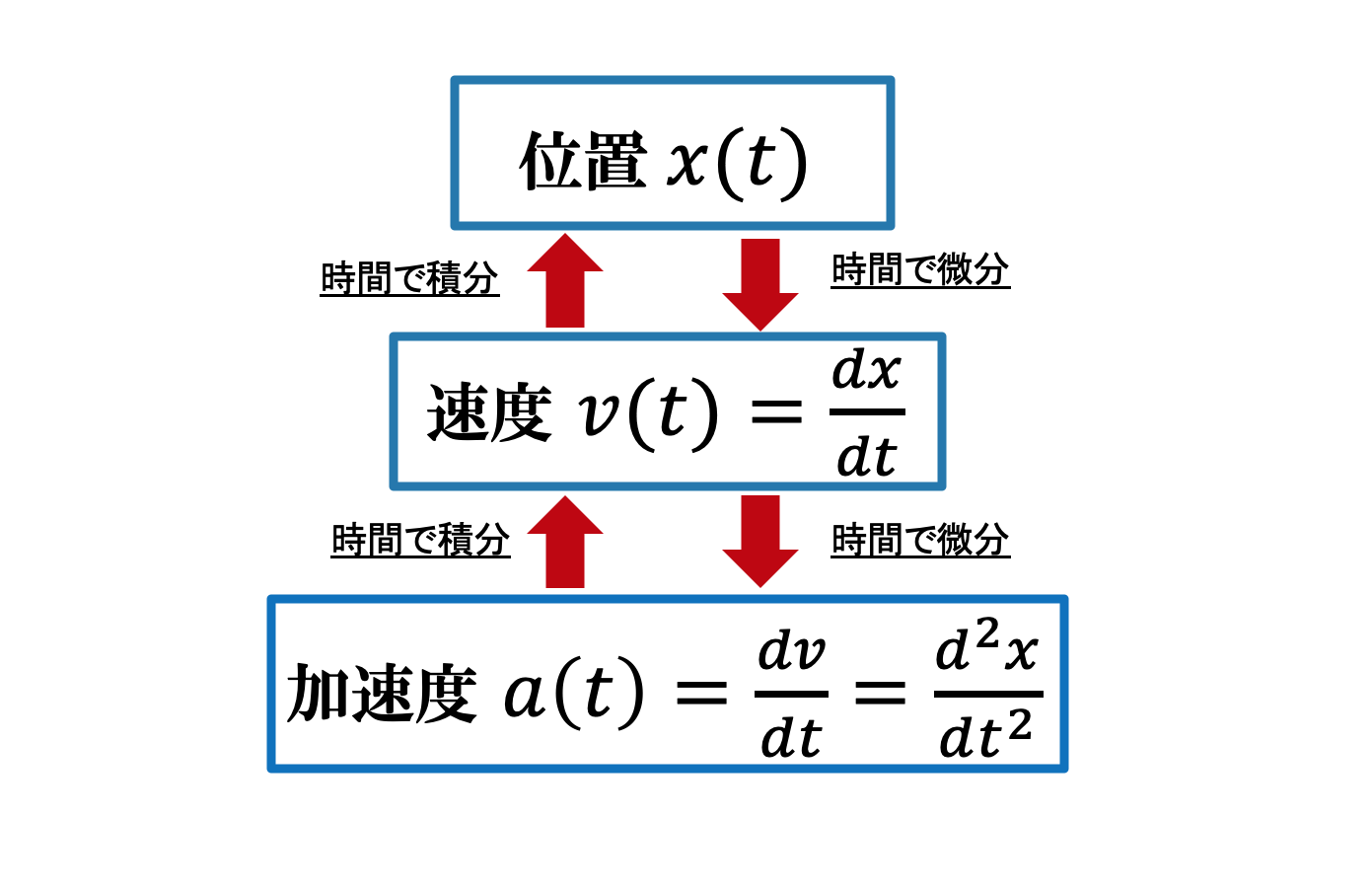
これらの関係を結論からいってしまうと
次のようになります。

上の関係がなぜ成り立つのか。
それが今回の話の核となるので
この点を意識して読んでいってください。
位置について
物理では位置のことを
変数$\large x$を用いて表します。
そしてこれは変位とも呼ばれたりしますが
とにかくこれは
物体がどこにあるのか
を表す変数だと理解しておいて下さい。
そして物理においてこれは
時間とともに変化
します。
つまり$\large x$は
時間の関数です。
位置を時間で微分すると、、
ではここで微分の内容を思い出してください。
(微分の内容がよくわからない方はこちら)
微分というのは次のように
ある一点での
傾きを求める操作
のことを言うのでした。

そしてこの「傾き」とは
点における変化の大きさ
のことです。
では
時間で微分する
場合にはどうなるかというと
ある瞬間での
変化の大きさ
を求める操作となります。
具体例として
次のような状況を思い浮かべてください。

このように物体が時刻$t_1$から$t_2$の間に
$x_1$から$x_2$へ移動したとしましょう。
この時、
物体の位置は平均で
毎秒どれぐらい変化したか
つまり
(平均の)速度
は
$$\Large \frac{x_2-x_1}{t_2-t_1}$$
の形で求まります。
ここで位置$x$の差を$\Delta x$
時間$t$の差を$\Delta t$とおくと
$$\Large \frac{\Delta x}{\Delta t}$$
ともかけます。
ではこの$t_2$を
どんどん$t_1$に近づけていく
とどうなるでしょうか。
これは言い換えると
$\Delta t$を0にどんどん近づける
(しかし決して0にしない)
操作とも言えます。
すると次の画像のように
$t_1$における瞬間の速度
を知ることができます。

そしてこの
ある瞬間の
速度を求める操作
は次のように微分を用いて
$$\Large \frac{dx}{dt}$$
とかけます。
(読み方は「ディーエックスディーティー」)
これは微分を解説した箇所でも解説したように
$d$はとても小さい数を表し
とても小さい
位置の変化$dx$を
とても小さい
時間の変化$dt$で割っている
というように見ることができます。
このようなわけで
$$\Large \frac{dx}{dt}$$
は
ある瞬間における
位置の変化の大きさ
つまり
ある瞬間における
物体の速度
を表せるわけです。
そしてこれは速度を$v(t)$として
$$\Large v(t)= \frac{dx}{dt}$$
とかけます。
速度について
速度$v$も位置と同様に
時間の関数です。
つまり速度も時間と共に変化し
ある時刻では5m/sだったのが
ある時刻では10m/sになったりしています。
速度に関しては位置$x$のように
静止画として視覚化できないので
ここは皆さんが想像力を働かす必要があります。
しかしやることとしては先ほどと
同じなので安心してください。
先ほど位置の瞬間の変化を
考えたのと同様に、次は
ある瞬間の
速度の変化
を考えていきましょう。
まずある時刻$t_1$と$t_2$における速度を
それぞれ$v_1$と$v_2$とすると
物体の速度は平均で
毎秒どれぐらい変化したか
つまり
(平均の)加速度
は
$$\Large \frac{v_2-v_1}{t_2-t_1}$$
と表せます。
そして$v_1$と$v_2$の差を$\Delta v$とおき
$t_1$と$t_2$の差を$\Delta t$とおくと
次のようにかけます。
$$\Large \frac{\Delta v}{\Delta t}$$
そして瞬間の速度の変化を見たいので
位置の場合と同様に
$t_2$をどんどん$t_1$に近づけていき
$\Delta t$を0に近づけていく場合を考えます。
これは
とても小さい
速度の変化を表す$dv$
と
とても小さい
時間の変化を表す$dt$
を用いて
$$\Large \frac{dv}{dt}$$
とかけます。
(読み方は「ディーブイディーティー」)
つまりこの式は
ある瞬間の
速度の変化の大きさ
を表しており、この変化の大きさを
加速度
と言うわけです。
加速度は通常$\large a$と書かれ
$$\Large a=\frac{dv}{dt}$$
のように書かれます。
位置、速度、加速度の関係まとめ
以上の関係を数式でまとめましょう。
この際次の事項を思い出してください。
微分は積分の逆の操作
積分は微分の逆の操作
(このことがピンとこない方は以下参照)
このことも考慮すると
位置と速度と加速度の関係は
次のようになります。

以上のような理由で
$x$を時間で微分すると
$v$になりますし
$v$を時間で微分すると
$a$になります。
逆に
$a$を時間で積分すると
$v$になりますし
$v$を時間で積分すると
$x$になるわけです。
加速度は位置$x$を2回微分している
ここで速度と加速度の関係
表す次の式を見てください。
$$\Large \frac{dv}{dt}=a(t)$$
ここに位置と速度の関係
を表す次の式を代入しましょう。
$$\Large v(t)=\frac{dx}{dt}$$
すると次のようになります。
$$\Large \frac{dv}{dt}=\frac{d}{dt}v(t)=a(t)$$
$$上式に\large v(t)=\frac{dx}{dt}を代入$$
$$\Large \frac{d}{dt} \frac{dx}{dt}=a(t)$$
つまり加速度については
位置を時間で1度微分し
もう1度時間で微分すると
加速度になる
ということが言えます。
そして上の表記はもっと簡潔に
$$\Large \frac{d^{2}x}{dt^2}=a(t)$$
というように表現され、これは
時間の2階微分
と呼ばれます。
これは次の記事で話す
運動方程式
で非常に重要となります。
表記の仕方
ここまで位置、速度、加速度の
時間の微分に基づく関係
について話してきました。
ここで速度は$v$
加速度は$a$のように書きましたが
通常他の書き方をします。
それは次のようなものです。
$$\Large v(t)=\dot{x} (t)$$
$$\Large a(t)=\ddot{x}(t)$$
上の点(ドット)の数は
時間で微分した
回数を表す
ということに気づけばすぐになれます。
読み方としては
「エックスドット」
「エックスツードット」
という感じです。
以後この表記を主に使っていくので忘れないように。

















コメントを残す