斜面上の物体に働く重力を分解すると「斜面の角度」が現れることの証明。

斜面の角度について成り立つ関係

斜面上にある物体について考える際、
重力は次のように分解されます。

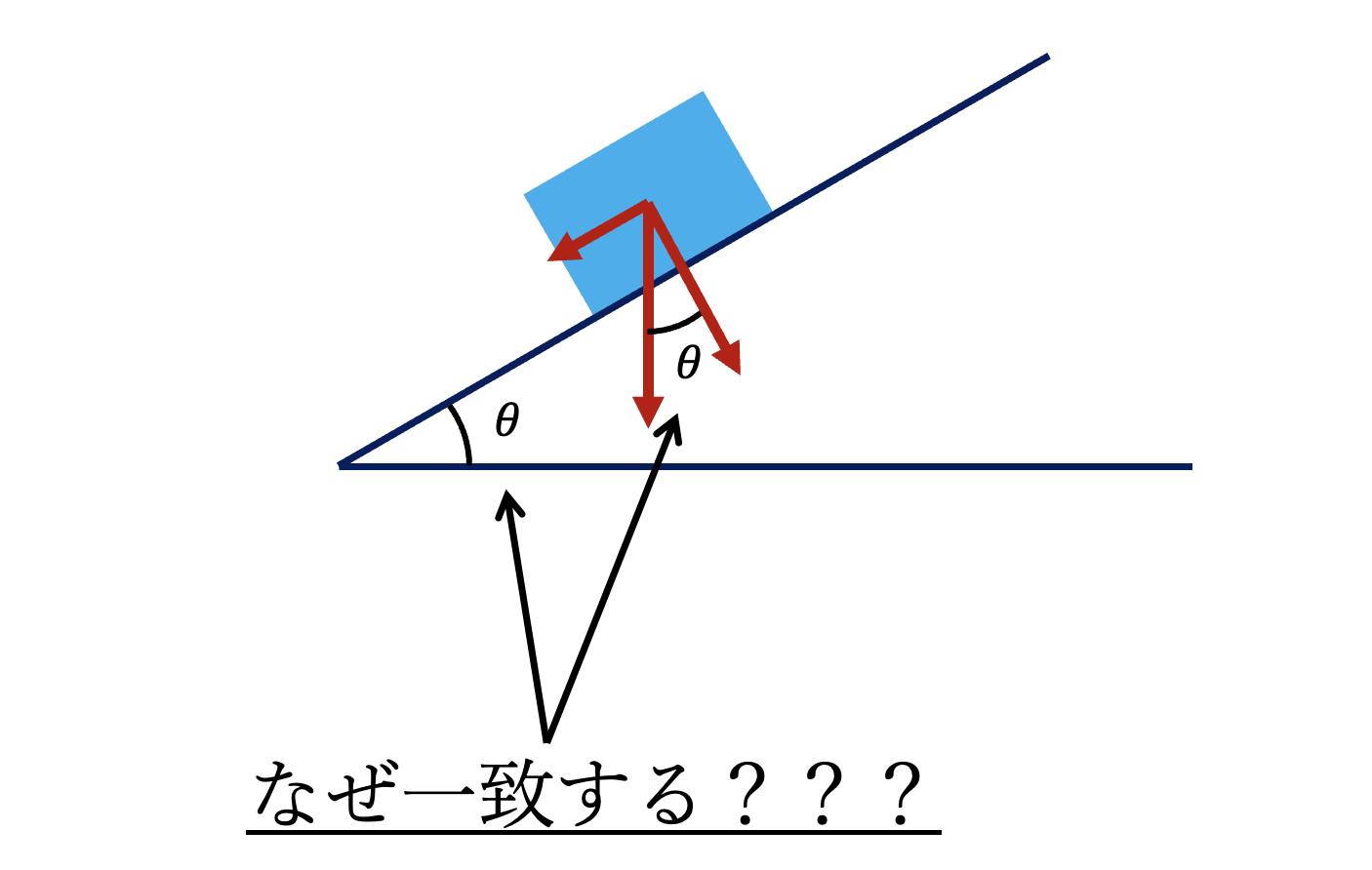
この図はおそらく見慣れているでしょう。

今回は上で現れた角度$\theta$について

なぜ2つの角度が
一緒になるのか？

をちゃんと証明していきます。

斜面の角度について成り立つ関係の証明

力を分解する

次のような
斜面上の物体を考えます。

今、斜面と物体の間に摩擦はないとすると
物体には重力のみが働きます。

力というのはどんな向きにでも分解できる
わけですが、一般的に、
斜面上の物体に働く重力を考える場合には

斜面に垂直な方向

と

斜面に並行な方向

という2つの方向に分解すると
考えやすいです。

ということで次のように
斜面に垂直な向きと斜面に平行な向きに
重力を分解します。

ここで角度●と角度❌について

$$\large ●+❌=\frac{\pi}{2}$$

となるように分解していることに
気をつけてください。

角度の関係の証明

再度、力を分解した図を示します。

上図において赤色の力は
斜面に平行です。

そのため錯角と同位角の関係から
次が成り立ちます。

（斜面に垂直な力は省略）

そのため、図より次の関係が成り立ちます。

$$\large \theta +❌=\frac{\pi}{2}$$

また上で示したように

$$\large ●+❌ = \frac{\pi}{2}$$

も成り立つのでした。

（再掲）

$$\large ●+❌ = \frac{\pi}{2}$$

$$\large \theta +❌=\frac{\pi}{2}$$

この2つの式を連立することで
容易に

$$\large ●=\theta$$

という式を得ることができます。

斜面の角度の関係は覚えてしまおう！

ここまで斜面の角度の関係を
図形的にちゃんと証明しましたが

物理の問題を解くときに逐一
この証明をやる必要はありません。

また、この関係を証明なしに
使っても原点されることも基本的にはありません。

逆にこの証明をやっていると
時間を無駄にしてしまいます。

なので普段は

暗記して、瞬時に
使えるようにしておく

ことをお勧めします。

上で解説した証明自体は
作図さえミスしなければ
さほど難しわけでもないので

聞かれたら答えられる

ぐらいにしておくといいです。

まとめ

それでは、今回のまとめです。