あの「微積物理」を無料で学べます！！
Contents
斜面への斜方投射の問題
今回考えるのは次のような問題です。
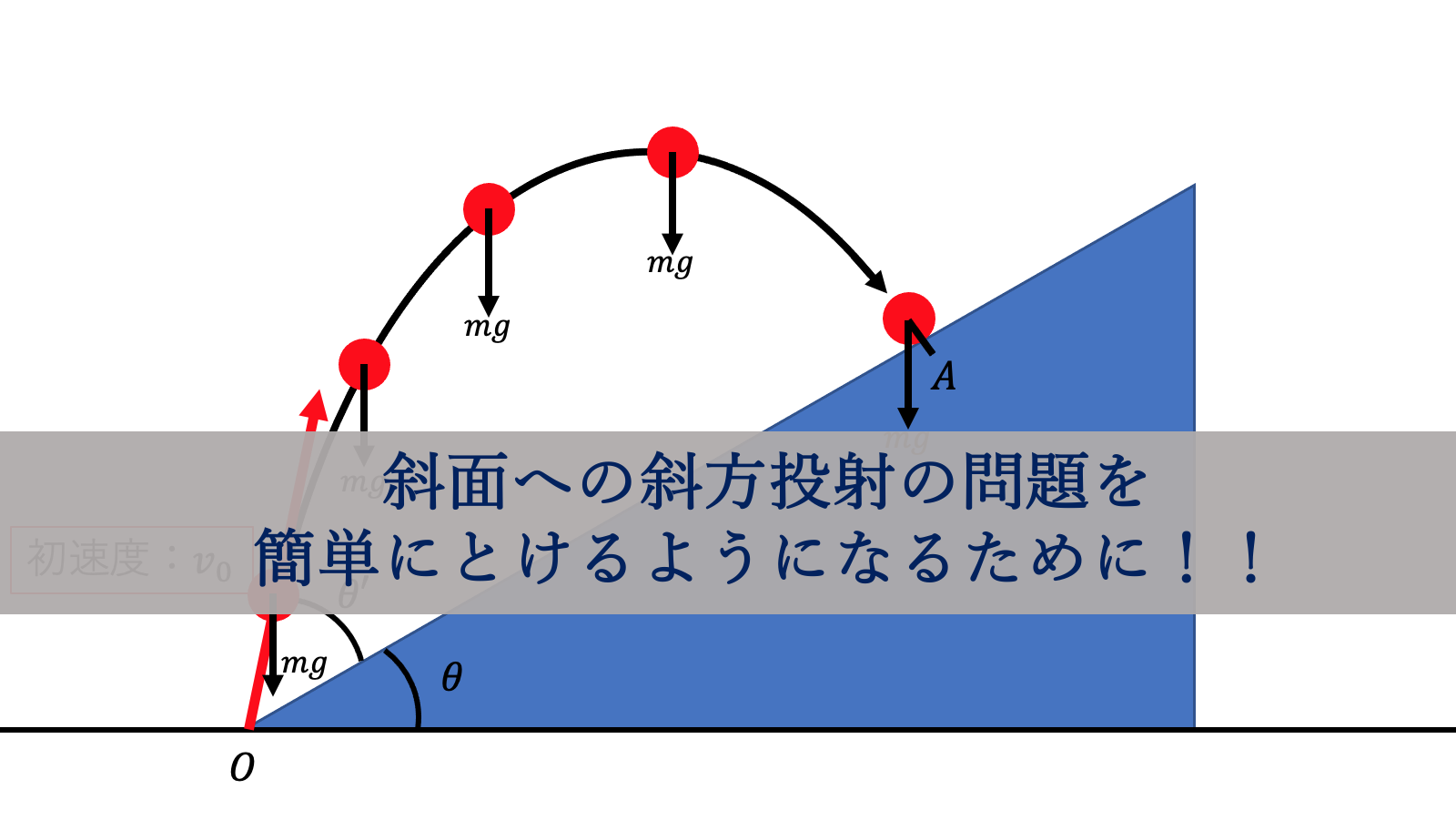
次の図に示すような
水平から$\theta$だけ傾き
地面に固定された斜面がある。
この斜面上の点Oから
斜面に対する打ち上げの角度を
$\theta’$として斜面の上に向かって初速度$v_0$で
物体を打ち出したところ
点Aで斜面に衝突した。
この時次の問いに答えよ。
- 物体を打ち上げてから
点Aにおいて
斜面に衝突するまでに
要する時間を求めよ。- 点Oと点Aの間の距離を求めよ。
- $\theta=\frac{\pi}{4}$に固定した時
点Aで物体は斜面に対して
垂直に衝突した。この時の斜面に対する
打ち上げの角度$\theta’$を用いた
$\tan\theta’$を求めよ。
斜方投射の問題に斜面が絡んだ
複雑な問題に見えるかもしれません。
しかし冷静に分解していけば
どうということはありません
働く力を考え、座標を取る
今回考えるべき力
それでは問題の図において
物体に働いている力
は何でしょうか？？
今回働いている力は
重力です。
それ以外に力は働いていないので
注意してください。
そして重力とは
みなさん経験的に知っているように
鉛直下向き
に働きます。
それ故、物体の質量を$m$として
図に重力を書き込むと
次のようになります。
座標を取る
では今回どのような座標を
取るといいでしょうか。
まず復習ですが、
斜面上の運動を考える時は
次の図のように
斜面に平行な軸と
斜面に垂直な軸からなる座標
が最適でした。
また、斜方投射を考える時には
つぎの図のように
鉛直上向きの軸と
水平方向の軸からなる座標
が最適でした。
今回の問題では
斜面と斜方投射が一緒になっているので
取るべき座標は先ほどあげた2つの座標を
足して2で割ったような座標になります。
そのような座標はつぎのようなものです。
ここで
と言う人がいるかもしれません。
そのような人は
力は2つの方向に
分解できる
ということを思い出してください。
つまり次のように
重力は軸に平行な
2つの力に分解できる
というわけです。
このように力は
自分の好きな方向に
分解できる
ことはしっかり
覚えておきましょう。
運動を分解する
先ほどは力を分解し
座標を設定したので
今度は
運動を分解
していきましょう。
$x$軸方向の運動
まず$x$軸方向の運動についてです。
$x$方向に働く力$F_x$は
重力を分解したもののうち
$x$方向を向いているものなので
$$\large F_x=-mg\sin\theta$$
となります。
このことを念頭に
物体の運動を
$x$軸に投影
してみましょう。
すると
となります。
上図で物体には
負の方向に力が働き
$x$軸にそって減速していきます。
つまり物体はx軸にそって
負の加速度で
等加速度運動
をするわけです。
運動方程式を立てると
その加速度$a$は
\begin{align}
ma&=F_x\\
\\
つまり\\
\large ma&=\large -mg\sin\theta\\
\\
\large a&=\large -g\sin\theta
\end{align}
となります。
$y$方向の運動
次に$y$軸方向の運動についてです。
$y$方向に働く力$F_y$は
重力を分解したもののうち
$y$方向を向いているものなので
$$\large F_y=-mg\cos\theta$$
となります。
このことを念頭に
先ほどと同様に
物体の運動を
$y$軸に投影
してみます。
すると
となります。
上図からわかるように
物体は$y$方向に投げ上げられ
その後落下してきます。
つまり物体は$y$軸にそって
鉛直投げ上げ運動
をするわけです。
ただ、今の場合その加速度は
重力速度$g$ではありません。
運動方程式を立てると
その加速度$a$は
\begin{align}
ma&=F_y\\
\\
つまり\\
\large ma&=\large -mg\cos\theta\\
\\
\large a&=\large -g\cos\theta
\end{align}
となります。
さぁこれで準備は整いました。
あとはこれまで学んだ
いろんな運動の公式を
組み合わせていくだけです。
問題を解いていく
- 物体を打ち上げてから点Aにおいて
斜面に衝突するまでに要する時間を求めよ。 - 点Oと点Aの間の距離を求めよ。
- $\theta=\frac{\pi}{4}$に固定した時
点Aで物体は斜面に対して垂直に衝突した。
この時の斜面に対する
打ち上げの角度$\theta’$を求めよ。
ではこの問題を解いていきましょう。
以下では等加速運動、また
鉛直投げ上げ運動そのものについては
詳しく解説しないので、自身のない方は
以下を参照してください。
問①斜面に衝突するまでに要する時間
斜面に衝突するということは
上で設定した座標において
再び$y=0$に戻って来る
ことを意味します。
そして$y$方向の運動は
鉛直投げ上げ運動に
等しかったのでした。
つまりこの問題は$y$方向の
鉛直投げ上げ運動において
戻って来るまでに
要する時間
を求めれば解けることになります。
今の場合、$y$方向の加速度は
$-g\cos\theta$となるので
次の等加速度運動の公式
$$y=v_0t+\frac{1}{2}at^2$$
に初速度として$v_0\sin\theta’$を
加速度として$-g\cos\theta$
を代入し、またy=0とおくことで
\begin{align}
0&=v_0\sin\theta’\cdot t -\frac{1}{2}g\cos\theta \cdot t^2\\
\\
0&=t(2v_0\sin\theta’-g\cos\theta \cdot t)\\
\\
&故に、\\
t&=0,\frac{2v_0\sin\theta’}{g\cos\theta}
\end{align}
最終的に求める答えは
$$\large t= \frac{2v_0\sin\theta’}{g\cos\theta}$$
となります。
（t=0は初期時刻であり、求めたいものでないことは明らか）
問②点Oと点Aの間の距離
これを知るためには
$x$方向の運動を考える
必要があるのは明らかでしょう。
そして$x$方向の運動は
（負の加速度の）
等加速度運動
であり、その加速度は
$-g\sin\theta$です。
また、その初速度は
$v_0\cos\theta’$です。
そのため$x$軸上の位置は
等加速度運動の次の公式
$$x=v_0t+\frac{1}{2}at^2$$
に、先程の加速度と
初速度を代入して
$$x=v_0\cos\theta’\cdot t- \frac{1}{2}g\sin\theta\cdot t^2$$
と表されます。
また斜面に落下するまでの時間は
問①で求めたので
その時間を上式に代入すれば
OAの距離が得られることになります。
実際に代入すると
\begin{align}
x&=v_0\cos\theta’\frac{2v_0\sin\theta’}{g\cos\theta}- \frac{1}{2}g\sin\theta \Big(\frac{2v_0\sin\theta’}{g\cos\theta}\Big)^2\\
\\
&=\frac{2v_0^2\sin\theta’}{g\cos^2\theta}\Big(\cos\theta \cos\theta’ – \sin\theta\sin\theta’\Big)\\
\\
&三角関数の和積の公式より\\
\\
&=\frac{2v_0^2\sin\theta’\cos(\theta+\theta’)}{g\cos^2\theta}
\end{align}
よって最終的にOAの距離は
$$\large OA=\frac{2v_0^2\sin\theta’\cos(\theta+\theta’)}{g\cos^2\theta}$$
と求まります。
問③$\tan\theta’$の値
改めて状況を整理します。
この場合斜面の角度$\theta$は
$\theta=\frac{\pi}{4}$です。
つまり次のようになります。
では
斜面に垂直に衝突した
とはどういうことでしょうか。
これを言い換えると
衝突の際
$x$方向の運動はない
ということなります。
そしてさらに言い換えると
衝突の際
$x$方向の速度は0であり
$y$方向の運動しかない
ということになります。
つまり問①で求めた次の時間
$$t= \frac{2v_0\sin\theta’}{g\cos\theta}$$
だけ時間が経過すると
物体の$x$方向の速度$v_x$
が0になっていればいいわけです。
等加速度運動の公式から
$$v_x=v_0+at$$
であるので、ここに
上で述べた時間$t$、
初速度$v_0\cos\theta’$、
加速度$-g\sin\theta$
また、$v_x=0$、$\theta=\frac{\pi}{4}$を代入していくと
\begin{align}
0&=v_0\cos\theta’-g\sin\frac{\pi}{4}\Big(\frac{2v_0\sin\theta’}{g\cos\frac{\pi}{4}}\Big)\\
\\
0&=v_0\cos\theta’-2v_0\sin\theta’\\
\\
\frac{\sin\theta’}{\cos\theta’}&=\frac{1}{2}\\
\\
\tan\theta’&=\frac{1}{2}
\end{align}
よって求める$\tan\theta’$は
$$\large \tan\theta’=\frac{1}{2}$$
だとわかります。
まとめ
それでは今回のまとめです。
- 斜面への斜方投射を考える際は
力と運動を2つの方向に分解して考える！ - 2つに分解した後、基本的な公式を組み合わせていく！
あの「微積物理」を無料で学べます！！
皆さんの「ここを教えてほしい」を募集しています！
高校物理に関して
「こんなことを教えて欲しい」
「この問題をわかりやすく解説して欲しい！」
「勉強のコツを知りたい！」
などなど、質問を募集しています！
気軽に質問してください！無料です！
質問内容に関しては記事として回答させていただきます！
⚠️質問の回答は先着順で回答していくため、質問から回答までの期間が長くなることがあります。あらかじめご了承ください。
重力と軸が平行ではない
じゃないですか！